题目内容
若函数f(x)(x∈R)是偶函数,函数g(x)(x∈R)是奇函数,则( )
| A、函数f[g(x)]是奇函数 |
| B、函数g[f(x)]是奇函数 |
| C、函数f(x)+g(x)是奇函数 |
| D、函数f(x)g(x)是奇函数 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:由条件可得f(-x)=f(x),g(-x)=-g(x),再把各个选项中的函数中的x换成-x,看它和原函数值是否相等或相反,从而根据函数的奇偶性的定义作出判断.
解答:
解:∵函数f(x)(x∈R)是偶函数,函数g(x)(x∈R)是奇函数,
∴f(-x)=f(x),g(-x)=-g(x),
∴f[g(-x)]=f[-g(x)]=f[g(x)],故函数f[g(x)]是偶函数,故排除A.
根据g[f(-x)]=g[f(x)]=g[f(x)],故函数g[f(x)]为偶函数,故排除B.
根据f(-x)+g(-x)=f(x)-g(x),故f(x)+g(x)为非奇非偶函数,故排除C.
根据f(-x)g(-x)=f(x)[-g(x)]=-f(x)g(x),显然函数f(x)g(x)是奇函数,
故选:D.
∴f(-x)=f(x),g(-x)=-g(x),
∴f[g(-x)]=f[-g(x)]=f[g(x)],故函数f[g(x)]是偶函数,故排除A.
根据g[f(-x)]=g[f(x)]=g[f(x)],故函数g[f(x)]为偶函数,故排除B.
根据f(-x)+g(-x)=f(x)-g(x),故f(x)+g(x)为非奇非偶函数,故排除C.
根据f(-x)g(-x)=f(x)[-g(x)]=-f(x)g(x),显然函数f(x)g(x)是奇函数,
故选:D.
点评:本题主要考查函数的奇偶性的判断方法,属于中档题.

练习册系列答案
相关题目
复数
等于( )
| 1 |
| i |
| A、-i | B、-1 | C、1 | D、i |
执行如图所示的程序框图,输出的S的值为( )


| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
等比数列{an}是递减数列,其前n项积为Tn,若T12=4T8,则a8•a13=( )
| A、±1 | B、±2 | C、1 | D、2 |
4名优秀学生A、B、C、D全部都被保送到甲、乙、丙3所学校,每所学校至少去一名,则不同的保送方案共有( )
| A、18种 | B、36种 |
| C、72种 | D、108种 |
程序框图(如图)的运算结果为( )


| A、2 | B、6 | C、18 | D、24 |
执行如图所示的程序框图,若输出的结果为2,则输入的正整数a的可能取值的集合是( )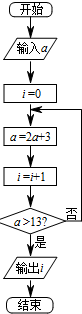

| A、{1,2,3,4,5} |
| B、{1,2,3,4,5,6} |
| C、{2,3,4,5} |
| D、{2,3,4,5,6} |
已知复数z1=2+i,z2=a-3i(i为虚数单位,a∈R).若z1•z2为实数,则a的值为( )
| A、3 | B、4 | C、5 | D、6 |