题目内容
已知3x2+2y2=6x,求x2+y2的范围.
考点:基本不等式
专题:三角函数的图像与性质,不等式的解法及应用,圆锥曲线的定义、性质与方程
分析:3x2+2y2=6x,化为(x-1)2+
=1,令x-1=cosθ,y=
sinθ.可得x2+y2=-
(cosθ-2)2+
,利用cosθ∈[-1,1],即可得出.
| y2 | ||
|
|
| 1 |
| 2 |
| 9 |
| 2 |
解答:
解:3x2+2y2=6x,化为(x-1)2+
=1,
令x-1=cosθ,y=
sinθ.
∴x2+y2=(cosθ+1)2+
sin2θ
=
sin2θ+2cosθ+2
=-
(cosθ-2)2+
,
∵cosθ∈[-1,1],
∴(cosθ-2)2∈[1,9],
∴(x2+y2)∈[0,4].
| y2 | ||
|
令x-1=cosθ,y=
|
∴x2+y2=(cosθ+1)2+
| 3 |
| 2 |
=
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 9 |
| 2 |
∵cosθ∈[-1,1],
∴(cosθ-2)2∈[1,9],
∴(x2+y2)∈[0,4].
点评:本题考查了椭圆的参数方程、三角函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
对任意实数a、b、c,给出下列命题:
①“a=b”是“ac=bc”的充要条件;
②“b2=ac”是“a,b,c成等比数列”的充要条件;
③“a<5”是“a<3”的必要条件;
④“a>b”是“a2>b2”的充分条件.
其中真命题的个数是( )
①“a=b”是“ac=bc”的充要条件;
②“b2=ac”是“a,b,c成等比数列”的充要条件;
③“a<5”是“a<3”的必要条件;
④“a>b”是“a2>b2”的充分条件.
其中真命题的个数是( )
| A、4 | B、3 | C、4 | D、1 |
已知集合U=R,M={x|2x>1},P={y|y=
},则( )
| 1-2x2 |
| A、P∩(CUM)={0} |
| B、P∪M=M |
| C、M∪(CUP)=R |
| D、M∩P=P |
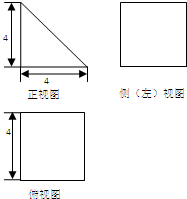 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为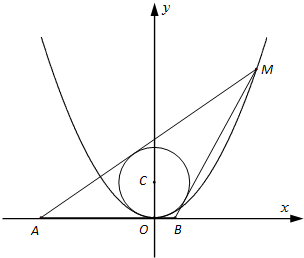 已知圆C:x2+(y-2)2=4,M(x0,y0)为抛物线x2=4y上的动点.
已知圆C:x2+(y-2)2=4,M(x0,y0)为抛物线x2=4y上的动点.