题目内容
已知点A，B，C的坐标分别是A（
，0），B（0，
），C（cosα，sinα）其中α∈（
，
），且A，B，C三点共线，求sin（π-α）+cos（π+α）的值．
| 1 |
| 5 |
| 1 |
| 5 |
| π |
| 2 |
| 3π |
| 2 |
考点：直线的斜率,运用诱导公式化简求值
专题：三角函数的求值
分析：利用向量共线定理可得sinα+cosα=
，再利用同角三角函数基本关系式可得sinα，cosα，利用诱导公式即可得出．
| 1 |
| 5 |
解答：
解：∵
=(-
，
)，
=(cosα-
，sinα)，A，B，C三点共线，
∴
(cosα-
)=-
sinα，
化为sinα+cosα=
，
∵α∈（
，
），sin2α+cos2α=1，
∴sinα=
，cosα=-
，
sin（π-α）+cos（π+α）
=sinα-cosα
=
-(-
)
=
．
| AB |
| 1 |
| 5 |
| 1 |
| 5 |
| AC |
| 1 |
| 5 |
∴
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
化为sinα+cosα=
| 1 |
| 5 |
∵α∈（
| π |
| 2 |
| 3π |
| 2 |
∴sinα=
| 4 |
| 5 |
| 3 |
| 5 |
sin（π-α）+cos（π+α）
=sinα-cosα
=
| 4 |
| 5 |
| 3 |
| 5 |
=
| 7 |
| 5 |
点评：本题考查了向量共线定理、同角三角函数基本关系式、诱导公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
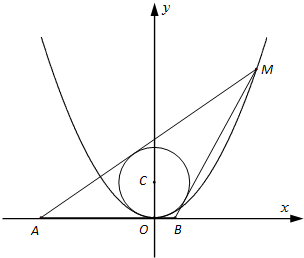已知圆C：x2+（y-2）2=4，M（x0，y0）为抛物线x2=4y上的动点．