题目内容
若z∈C,且(1+i)z=3+4i,则复数z的虚部是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则、虚部的定义即可得出.
解答:
解:∵(1+i)z=3+4i,
∴z=
=
=
,
其虚部为
.
故选:B.
∴z=
| 3+4i |
| 1+i |
| (3+4i)(1-i) |
| (1+i)(1-i) |
| 7+i |
| 2 |
其虚部为
| 1 |
| 2 |
故选:B.
点评:本题考查了复数的运算法则、虚部的定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(理科)已知z=a+bi(a、b∈R,i是虚数单位),z1,z2∈C,定义:D(z)=||z||=|a|+|b|,D(z1,z2)=||z1-z2||.给出下列命题:
(1)对任意z∈C,都有D(z)>0;
(2)若
是复数z的共轭复数,则D(
)=D(z)恒成立;
(3)若D(z1)=D(z2)(z1、z2∈C),则z1=z2;
(4)对任意z1、z2、z3∈C,结论D(z1,z3)≤D(z1,z2)+D(z2,z3)恒成立,
则其中真命题是( )
(1)对任意z∈C,都有D(z)>0;
(2)若
. |
| z |
. |
| z |
(3)若D(z1)=D(z2)(z1、z2∈C),则z1=z2;
(4)对任意z1、z2、z3∈C,结论D(z1,z3)≤D(z1,z2)+D(z2,z3)恒成立,
则其中真命题是( )
| A、(1)(2)(3)(4) |
| B、(2)(3)(4) |
| C、(2)(4) |
| D、(2)(3) |
已知集合U=R,M={x|2x>1},P={y|y=
},则( )
| 1-2x2 |
| A、P∩(CUM)={0} |
| B、P∪M=M |
| C、M∪(CUP)=R |
| D、M∩P=P |
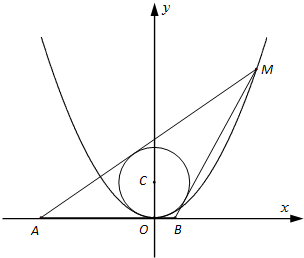 已知圆C:x2+(y-2)2=4,M(x0,y0)为抛物线x2=4y上的动点.
已知圆C:x2+(y-2)2=4,M(x0,y0)为抛物线x2=4y上的动点.