题目内容
“mn<0”是方程mx2+ny2=1表示双曲线的( )条件.
| A、充分不必要 | B、必要不充分 |
| C、充要 | D、不充分不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:推理和证明
分析:由充要条件的证明,结合双曲线方程的特点证明即可.
解答:
解:若“mn<0”,则m、n均不为0,方程mx2+ny2=1,可化为
+
=1,
由“mn<0”可得
、
异号,方程表示双曲线,
故“mn<0”是方程“mx2+ny2=1表示双曲线”的充分条件;
反之,若mx2+ny2=1表示双曲线,则其方程可化为为
+
=1,
此时有
、
异号,则必有mn<0,
故“mn<0”是方程“mx2+ny2=1表示双曲线”的必要条件;
综合可得:“mn<0”是方程“mx2+ny2=1表示双曲线”的充要条件;
故选:C.
| x2 | ||
|
| y2 | ||
|
由“mn<0”可得
| 1 |
| m |
| 1 |
| n |
故“mn<0”是方程“mx2+ny2=1表示双曲线”的充分条件;
反之,若mx2+ny2=1表示双曲线,则其方程可化为为
| x2 | ||
|
| y2 | ||
|
此时有
| 1 |
| m |
| 1 |
| n |
故“mn<0”是方程“mx2+ny2=1表示双曲线”的必要条件;
综合可得:“mn<0”是方程“mx2+ny2=1表示双曲线”的充要条件;
故选:C.
点评:本题考查双曲线的方程形式与充分必要条件的判断,关键在于掌握二元二次方程mx2+ny2=1表示双曲线条件,属基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
已知x与y成线性相关,其统计数据如下表:
则x与y的线性回归方程
=
x+
必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
| A、(2,2) |
| B、(1.5,4) |
| C、(1.5,0) |
| D、(1,2) |
m∈R,复数(2m2-3m-2)+(m2-3m+2)i表示纯虚数的充要条件是( )
A、m=-
| ||
| B、m=2 | ||
C、m=-
| ||
| D、m=2或m=1 |
如图所示为一简谐振动的图象,则下列判断正确的是( )
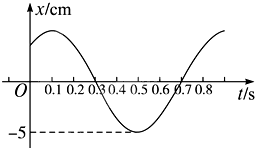

| A、该质点的振动周期为0.7s |
| B、该质点的振幅为5cm |
| C、该质点在0.1s和0.5s时振动速度最大 |
| D、该质点在0.3s和0.7s时的加速度为零 |
已知扇形的弧长为l,半径为r.类比三角形的面积公式:S=
底×高,可推知扇形的面积公式S扇形等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、lr |
已知实数a,b满足a>b,则下列说法一定正确的是( )
| A、a-c>b-c | ||||
| B、a2>b2 | ||||
C、
| ||||
| D、ac2>bc2 |
设△ABC的三个内角A,B,C所对的边分别是a,b,c,已知A=60°,a=
,c=
,则b=( )
| 6 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、3 |
已知tan(π-a)=2,则
=( )
| 1 |
| sinαcosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|