题目内容
假设乒乓球团体比赛的规则如下:进行5场比赛,除第三场为双打外,其余各场为单打,参赛的每个队选出3名运动员参加比赛,每个队员打两场,且第1、2场与第4、5场不能是某个运动员连续比赛.某队有4名乒乓球运动员,其中A不适合双打,则该队教练安排运动员参加比赛的方法共有 种.
考点:计数原理的应用
专题:排列组合
分析:将4名运动员分别记为A、B、C、D:分两种情况考虑,第一种是4选3时没有选到A,第二种是4选3时选到了A,结合比赛规则分别讨论两种情况下的参赛安排情况,最后综合讨论结果,可得答案.
解答:
解:将4名运动员分别记为A、B、C、D:分两种情况考虑,第一种是4选3时没有选到A,第二种是4选3时选到了A.
第一种情况:4选3时没有选到A,则B、C、D参加比赛
第一场单打比赛的安排方法有3种,
第二场单打比赛的安排方法有2种,
第三场双打比赛的安排方法有2种(因为打了一二场的两名选手不能组合打双打,否则第4、5两场就是一人连打了),
第四场单打比赛的安排方法有2种,
第五场单打比赛的安排方法有1种,
共有3×2×2×2×1=24种安排方法.
第二种情况:4选3时选到了A,则有ABC、ABD、ACD三种选法,对于每一种选法,都有:
第三场双打比赛的安排方法有1种,
A必在1、2场中选一场,有两种选法,再在4、5场中选一场,有两种选法,
当A选择了1、2场后,剩下一场有两种选法,4、5中剩下的一场只有一种选法了.
共有3×2×2×2×1=24种安排方法.
故总的安排方法有24+24=48种.
故答案为:48.
第一种情况:4选3时没有选到A,则B、C、D参加比赛
第一场单打比赛的安排方法有3种,
第二场单打比赛的安排方法有2种,
第三场双打比赛的安排方法有2种(因为打了一二场的两名选手不能组合打双打,否则第4、5两场就是一人连打了),
第四场单打比赛的安排方法有2种,
第五场单打比赛的安排方法有1种,
共有3×2×2×2×1=24种安排方法.
第二种情况:4选3时选到了A,则有ABC、ABD、ACD三种选法,对于每一种选法,都有:
第三场双打比赛的安排方法有1种,
A必在1、2场中选一场,有两种选法,再在4、5场中选一场,有两种选法,
当A选择了1、2场后,剩下一场有两种选法,4、5中剩下的一场只有一种选法了.
共有3×2×2×2×1=24种安排方法.
故总的安排方法有24+24=48种.
故答案为:48.
点评:本题主要考查排列与组合,若题目要求元素的顺序则是排列问题,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素,属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
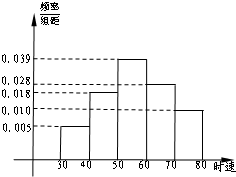 5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )
5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )| A、50 | B、500 |
| C、1000 | D、4500 |
设向量
=(x,0),
=(x-2,1),集合A={x|
•
≥0},B={x|0<x<4},则A∩B=( )
| a |
| b |
| a |
| b |
| A、[2,4) |
| B、(2,4) |
| C、(-∞,4) |
| D、(-∞,0] |
 已知某几何体的三视图如图所示,其中正视图是直角三角形,侧视图是正三角形,俯视图是边长为2的正方形,则此几何体的表面积为
已知某几何体的三视图如图所示,其中正视图是直角三角形,侧视图是正三角形,俯视图是边长为2的正方形,则此几何体的表面积为