题目内容
19.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$,则|$\overrightarrow{b}$|=3$\sqrt{5}$.分析 对|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$两边平方,解方程即可.
解答 解:${\overrightarrow{a}}^{2}$=5,∵|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$,∴${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=50,
即5+${\overrightarrow{b}}^{2}$=50,∴${\overrightarrow{b}}^{2}$=45.
∴|$\overrightarrow{b}$|=$\sqrt{45}$=3$\sqrt{5}$.
故答案为3$\sqrt{5}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.已知集合A={x|y=$\sqrt{x+1}$},B={y|y<1},则A∩B=( )
| A. | (-1,1) | B. | [-1,1] | C. | [-1,1) | D. | (-∞,-1]∪[1,+∞) |
20.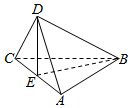 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )| A. | 直线AB⊥直线CD,且直线AC⊥直线BD | |
| B. | 直线AB⊥平面BCD,且直线AC⊥平面BDE | |
| C. | 平面ABC⊥平面BDE,且平面ACD⊥BDE | |
| D. | 平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
1.幂函数y=f(x)的图象经过点(2,4),则f(x)的解析式为( )
| A. | f(x)=2x | B. | f(x)=x2 | C. | f(x)=2x | D. | f(x)=log2x+3 |