题目内容
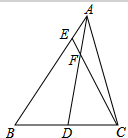如图，在△ABC中，AD 是BC边上的中线，F是AD上的一点，且| AF |
| FD |
| 1 |
| 5 |
| AE |
| EB |
考点：相似三角形的性质
专题：立体几何
分析：过点D作EC的平行线，得到BE的中点G，再利用平行线分线段成比例定理，得到：
=
，进而求得答案．
| AE |
| EG |
| AF |
| FD |
解答：
解：如图所示，过点D作EC的平行线，交AB于G，
∵AD 是BC边上的中线，
∴D为BC的中点，
∴G是BE的中点，
∵DG∥EC，
∴
=
=
，
∴
=
=
故答案为：
∵AD 是BC边上的中线，
∴D为BC的中点，
∴G是BE的中点，
∵DG∥EC，
∴
| AE |
| EG |
| AF |
| FD |
| 1 |
| 5 |
∴
| AE |
| EB |
| AE |
| 2EG |
| 1 |
| 10 |
故答案为：
| 1 |
| 10 |
点评：本题考查的知识点是平行线分线段成比例定理，添加辅助线DG是解答的关键．
练习册系列答案
相关题目
过抛物线x2=y焦点的直线l交抛物线于A、B两点，且|AB|=4，则线段AB中点到x轴的距离是（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
对函数f（x），若存在区间M=[a，b]（a＜b），使得{y|y=f（x），x∈M}=M，则称区间M为函数f（x）的一个“稳定区间”，给出下列四个函数：
（1）f（x）=ex，（2）f（x）=x3，（3）f（x）=cos
x，（4）f（x）=lnx+1，
其中存在“稳定区间”的函数有（ ）
（1）f（x）=ex，（2）f（x）=x3，（3）f（x）=cos
| π |
| 2 |
其中存在“稳定区间”的函数有（ ）
| A、（1）（2） |
| B、（2）（3） |
| C、（3）（4） |
| D、（1）（4） |
已知F1、F2是椭圆
+
=1（a＞b＞0）的左、右焦点，过F2且垂直于x轴的直线与椭圆交于A、B两点，若△ABF1是锐角三角形，则该椭圆离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、e＞
| ||||
B、0＜e＜
| ||||
C、
| ||||
D、
|