题目内容
在△ABC中，已知AD为BC边上的高，BD=2DC，若
=λ
+μ
，则4λ-μ=的值为 ．
| AD |
| AB |
| AC |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：过点D作DE∥AC，交AC于E，过点D作DF∥AB，交AC于F，由题设条件知
=
，
=
，由此结合图形给求出结果．
| ED |
| 2 |
| 3 |
| AC |
| FD |
| 1 |
| 3 |
| AB |
解答：
解：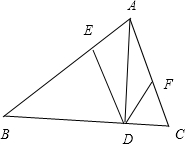
如图，过点D作DE∥AC，交AC于E，
过点D作DF∥AB，交AC于F，
∵AD为BC边上的高，BD=2DC，
∴
=
，
=
，
∵
=
+
=
+
=
+
AC，
=λ
+μ
，
∴λ=
，μ=
，
∴4λ-μ=
-
=
．
故答案为：
．
如图，过点D作DE∥AC，交AC于E，过点D作DF∥AB，交AC于F，
∵AD为BC边上的高，BD=2DC，
∴
| ED |
| 2 |
| 3 |
| AC |
| FD |
| 1 |
| 3 |
| AB |
∵
| AD |
| AE |
| ED |
| FD |
| ED |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AD |
| AB |
| AC |
∴λ=
| 1 |
| 3 |
| 2 |
| 3 |
∴4λ-μ=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查平面向量加法的运算法则的应用，是基础题，解题时要注意数形结合思想的合理运用．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知边长为
的正方形ABCD的对角线BD上任意取一点P，则
•(
+
的取值范围是（ ）
| 2 |
| PB |
| PA |
| PC) |
| A、[0，1] | ||
B、[0，
| ||
| C、[-4，0] | ||
D、[-
|