题目内容
已知向量
、
满足：|
|=1，|
|=2，且
、
的夹角为60°．
（Ⅰ）求
+
的模；
（Ⅱ）若λ
-6
与λ
+
互相垂直，求λ的值．
| a |
| b |
| a |
| b |
| a |
| b |
（Ⅰ）求
| a |
| b |
（Ⅱ）若λ
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（Ⅰ）|
+
|=
=
，由此根据已知条件能求出
+
的模．
（Ⅱ）由向量垂直数量积为0，利用题设条件，能求出λ的值．
| a |
| b |
(
|
|
| a |
| b |
（Ⅱ）由向量垂直数量积为0，利用题设条件，能求出λ的值．
解答：
解：（Ⅰ）∵|
|=1，|
|=2，且
、
的夹角为60°，
∴|
+
|=
=
=
=
．…（6分）
（Ⅱ）∵λ
-6
与λ
+
互相垂直，
∴(λ
-6
)•(λ
+
)=0，
∴λ2
2-5λ
•
-6
2=0，
∴λ2-5λ-24=0，
解得λ=8或λ=-3．…（13分）
| a |
| b |
| a |
| b |
∴|
| a |
| b |
(
|
|
=
| 1+4+2×1×2×cos60° |
=
| 7 |
（Ⅱ）∵λ
| a |
| b |
| a |
| b |
∴(λ
| a |
| b |
| a |
| b |
∴λ2
| a |
| a |
| b |
| b |
∴λ2-5λ-24=0，
解得λ=8或λ=-3．…（13分）
点评：本题考查向量的模的求法，考查向量垂直的条件的应用，是基础题，解题时要熟练掌握向量的数量积的运算．
练习册系列答案
相关题目
已知边长为
的正方形ABCD的对角线BD上任意取一点P，则
•(
+
的取值范围是（ ）
| 2 |
| PB |
| PA |
| PC) |
| A、[0，1] | ||
B、[0，
| ||
| C、[-4，0] | ||
D、[-
|
已知集合A={2，0，1，4}，集合B={x|0＜x≤4，x∈R}，集合C=A∩B．则集合C可表示为（ ）
| A、{2，0，1，4} |
| B、{1，2，3，4} |
| C、{1，2，4} |
| D、{x|0＜x≤4，x∈R} |
已知向量
=（sinα，cos2α），
=（1-2sinα，-1），α∈（
，
），若
•
=-
，则tan(α-
)的值为（ ）
| a |
| b |
| π |
| 2 |
| 3π |
| 2 |
| a |
| b |
| 8 |
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
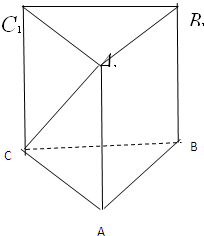如图三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°，