题目内容
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)若椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(文)(Ⅱ)在(Ⅰ)的条件下,设过点F且斜率不为0的直线交椭圆C于A、B两点,试问X轴上是否存在定点P,使PF平分∠APB?若存在,求出点P的坐标;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设M,N为短轴的两个三等分点,由△MNF为正三角形解得b=
,a2=b2+1=4,由此可求椭圆方程.
(Ⅱ)设线AB的方程与椭圆C的方程联立,利用韦达定理,结合PM平分∠APB,则直线PA,PB的倾斜角互补,建立方程,即可求得结论.
| 3 |
(Ⅱ)设线AB的方程与椭圆C的方程联立,利用韦达定理,结合PM平分∠APB,则直线PA,PB的倾斜角互补,建立方程,即可求得结论.
解答:
解:(Ⅰ)设M,N为短轴的两个三等分点,
因为△MNF为正三角形
所以|OF|=
|MN|,即1=
•
,
解得b=
,a2=b2+1=4,
因此,椭圆方程为
+
=1.
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为x=my+1.
将直线AB的方程与椭圆C的方程联立,消去x得(3m2+4)y2+6my-9=0.
所以△>0,y1+y2=-
,y1y2=-
.
若PM平分∠APB,则直线PA,PB的倾斜角互补,所以kPA+kPB=0.
设P(a,0),则有kPA=
,kPB=
,
+
=0,
将x1=my1+1,x2=my2+2代入上式,
整理得
,
所以 2my1y2+(1-a)(y1+y2)=0.
将y1+y2=-
,y1y2=-
代入上式,整理得(6a-24)•m=0.
由于上式对任意实数m都成立,所以a=4.
综上,存在定点P(4,0),使PM平分∠APB.
因为△MNF为正三角形
所以|OF|=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
解得b=
| 3 |
因此,椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为x=my+1.
将直线AB的方程与椭圆C的方程联立,消去x得(3m2+4)y2+6my-9=0.
所以△>0,y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
若PM平分∠APB,则直线PA,PB的倾斜角互补,所以kPA+kPB=0.
设P(a,0),则有kPA=
| y1 |
| x1-a |
| y2 |
| x2-a |
| y1 |
| x1-a |
| y2 |
| x2-a |
将x1=my1+1,x2=my2+2代入上式,
整理得
| 2my1y2+(1-a)(y1+y2) |
| (my1+1-a)(my2+1-a) |
所以 2my1y2+(1-a)(y1+y2)=0.
将y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
由于上式对任意实数m都成立,所以a=4.
综上,存在定点P(4,0),使PM平分∠APB.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查存在性问题的探究,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知
=(-3,4)与
=(6,x)共线,则x=( )
| a |
| b |
| A、8 | ||
| B、-8 | ||
C、
| ||
D、-
|
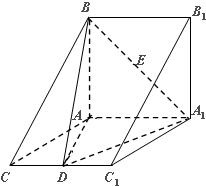 如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.
如图在三棱柱ABC-A1B1C1中,平面ABB1A1⊥平面AA1C1C,∠BAA1=90°,∠CAA1=120°,AB=AC=AA1=2,D是棱CC1的中心点.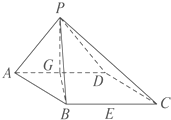 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
