题目内容
13.已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.根据表中数据,得到K2的观测值k=$\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}$≈4.844,则有95%的把握认为选修文科与性别有关.| 理科 | 文科 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
分析 K2≈4.844>3.841,根据P(K2≥3.841)≈0.05,这表明小概率事件发生,利用假设检验的基本原理,可得结论.
解答 解:由K2的观测值k=$\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}$≈4.844>3.841,
∴P(K2≥3.841)≈0.05,这表明小概率事件发生,根据假设检验的基本原理,
应该断定“是否选修文科与性别之间有关系”成立,选修文科与性别有关系的可能性不低于95%.
故答案为:95%.
点评 本题考查独立性检验,列联表,属于简单题.

练习册系列答案
相关题目
3.下列各式正确的是( )
| A. | arctan(-1)=$\frac{3π}{4}$ | B. | arctan($\frac{1}{2}$)=$\frac{π}{6}$ | C. | arcsin(-$\frac{1}{2}$)=-$\frac{π}{6}$ | D. | arccos(-$\frac{1}{2}$)=-$\frac{π}{3}$ |
1.网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )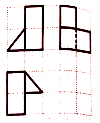

| A. | 2 | B. | 4 | C. | $\frac{2\sqrt{2}}{3}$ | D. | 1+$\frac{2\sqrt{2}}{3}$ |
8.观察下列各式:55=3 125,56=15 625,57=78 125,58=390 625,59=1 953 125,…,则585的末四位数字为( )
| A. | 3125 | B. | 5625 | C. | 8125 | D. | 0625 |
5.执行如图的程序框图,输出S的值是( )


| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
2.已知a,b,c∈R,则下列推证中正确的是( )
| A. | a>b⇒am2>bm2 | B. | $\frac{a}{c}>\frac{b}{c}$⇒a>b | ||
| C. | ac2>bc2⇒a>b | D. | a2>b2,ab>0⇒$\frac{1}{a}<\frac{1}{b}$ |
9. 某三棱锥的三视图如图所示,其中俯视图是一个等腰直角三角形,则该三棱锥的外接球的表面积为( )
某三棱锥的三视图如图所示,其中俯视图是一个等腰直角三角形,则该三棱锥的外接球的表面积为( )
 某三棱锥的三视图如图所示,其中俯视图是一个等腰直角三角形,则该三棱锥的外接球的表面积为( )
某三棱锥的三视图如图所示,其中俯视图是一个等腰直角三角形,则该三棱锥的外接球的表面积为( )| A. | 5π | B. | $\sqrt{5}$π | C. | $\frac{5π}{3}$ | D. | $\frac{{5\sqrt{5}π}}{6}$ |