题目内容
为了解儿子身高与其父亲身高的关系，随机抽取5对父子的身高数据如下：
则y对x的线性回归方程为（ ）
| 父亲身高x（cm） | 174 | 175 | 176 | 176 | 179 |
| 儿子身高y（cm） | 175 | 175 | 176 | 177 | 177 |
| A、y=x-1 | ||
| B、y=x+1 | ||
C、y=88+
| ||
D、y=176+
|
考点：线性回归方程
专题：概率与统计
分析：根据所给的数据计算出x，y的平均数和回归直线的斜率，即可写出回归直线方程．
解答：
解：∵
=
=176，
=
=176，
∴样本组数据的样本中心点是（176，176），
b=
=
，a=
-b
=88，
∴回归直线方程为：y=88+
x．
故选：C．
. |
| x |
| 174+175+176+176+179 |
| 5 |
. |
| y |
| 175+175+176+177+177 |
| 5 |
∴样本组数据的样本中心点是（176，176），
b=
| |||||||
|
| 1 |
| 2 |
. |
| y |
. |
| x |
∴回归直线方程为：y=88+
| 1 |
| 2 |
故选：C．
点评：本题考查回归分析的初步应用，写方程要用的斜率和x，y的平均数都要经过计算算出，这样的题有一定的运算量，是一个基础题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
我们把离心率为黄金比
的椭圆称之为“优美椭圆”．设F1、F2是“优美椭圆”C：
+
=1（a＞b＞0）的左、右焦点，则椭圆C上满足∠F1PF2=90°的点P的个数为（ ）
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、0 | B、2 |
| C、4 | D、以上答案均不正确 |
直线2ay-x=0与直线（3a-1）x-ay-1=0平行且不重合，则a等于（ ）
A、
| ||
B、
| ||
C、0或
| ||
D、0或
|
cos75°cos105°+sin75°sin105°的值是（ ）
| A、-1 | ||||
B、-
| ||||
C、
| ||||
D、
|
若圆的方程为
（θ为参数），当θ=
时，对应点的坐标是（ ）
|
| π |
| 2 |
| A、（2，0） |
| B、（0，2） |
| C、（-2，0） |
| D、（0，-2） |
直线y=5，与y=-1在区间[0，
]上截曲线y=Asinωx+B（A＞0，B＞0，ω＞0）所得弦长相等且不为零，则下列描述正确的是（ ）
| 2π |
| ω |
A、A≤
| ||||
| B、A≤3，B=2 | ||||
C、A＞
| ||||
| D、A＞3，B=2 |
直线l1：（
-1）x+y-2=0与直线l2：（
+1）x-y-3=0的位置关系是（ ）
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |
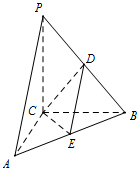如图，在三棱锥P-ABC中，PB⊥AC，PC⊥平面ABC，点D，E分别为线段PB，AB的中点．