题目内容
设正数P1,P2,…P2n满足P1+P2+P3+…+P2n=1,求证:p1log2p1+p2log2p2+P3log2P3+…+p2nlog2p2n≥-n.
考点:对数的运算性质
专题:函数的性质及应用
分析:构造函数g(x)=xlog2x-x+1,可得g′(x)=log2x+
-1,则当x≥1时,log2x≥0,
-1>0,利用导数研究其单调性可得xlog2x≥x-1.令x=2nPi,则有2nPilog2(2nPi)≥2nPi-1,两边同除以2n,可得,Pilog2(2nPi)≥Pi-
,利用“累加求和”化简整理即可得出.
| 1 |
| ln2 |
| 1 |
| ln2 |
| 1 |
| 2n |
解答:
证明:构造函数g(x)=xlog2x-x+1,
∴g′(x)=log2x+
-1,则当x≥1时,log2x≥0,
-1>0,
∴当x≥1时,g′(x)>0,即g(x)在[1,+∞)上是增函数,
∴g(x)≥g(1)=0,即xlog2x-x+1≥0,
∴xlog2x≥x-1.
令x=2nPi,则有2nPilog2(2nPi)≥2nPi-1,两边同除以2n,可得,Pilog2(2nPi)≥Pi-
,
利用“累加求和”可得:p1log2(2np1)+p2log2(2nP2)+P3log2(2nP3)+…+P2nlog2(2nP2n)≥p1+p2+…+P2n-1,
化简可得,(P1+P2+…+P2n)log2(2n)+P1log2P1+…+P2nlog2P2n≥(P1+P2+…+P2n)-1•
∵P1+P2+…P2n=1,
∴log2(2n)+P1log2P1+…+P2nlog2P2n≥0,
∴n+P1log2P1+…+P2nlog2P2n≥0,
∴P1log2P1+…+P2nlog2P2n≥-n.
∴g′(x)=log2x+
| 1 |
| ln2 |
| 1 |
| ln2 |
∴当x≥1时,g′(x)>0,即g(x)在[1,+∞)上是增函数,
∴g(x)≥g(1)=0,即xlog2x-x+1≥0,
∴xlog2x≥x-1.
令x=2nPi,则有2nPilog2(2nPi)≥2nPi-1,两边同除以2n,可得,Pilog2(2nPi)≥Pi-
| 1 |
| 2n |
利用“累加求和”可得:p1log2(2np1)+p2log2(2nP2)+P3log2(2nP3)+…+P2nlog2(2nP2n)≥p1+p2+…+P2n-1,
化简可得,(P1+P2+…+P2n)log2(2n)+P1log2P1+…+P2nlog2P2n≥(P1+P2+…+P2n)-1•
∵P1+P2+…P2n=1,
∴log2(2n)+P1log2P1+…+P2nlog2P2n≥0,
∴n+P1log2P1+…+P2nlog2P2n≥0,
∴P1log2P1+…+P2nlog2P2n≥-n.
点评:本题考查了通过构造函数研究函数的单调性证明不等式的方法,考查了“累加求和”方法与对数的运算性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
“k>9”是“
+
=1表示双曲线”的( )
| x2 |
| 9-k |
| y2 |
| 4+k |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知A={0,1,2,3},B={x|x≤
},A∩B等于( )
| 3 |
| A、{0} |
| B、{0,1} |
| C、{0,1,2} |
| D、{1,2,3} |
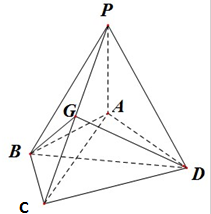 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=