题目内容

已知直线l1：ax+2y+1=0与直线l2：x+（3-a）y+a=0，若l1∥l2，则a的值为（　　）
A、1B、2C、6D、1或2
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：把直线方程化为斜截式，利用直线平行与斜率、截距的关系即可得出．
解答： 解：把直线方程分别化为：y=-
a
2
x-
1
2
，y=
1
a-3
x+
a
a-3
，
∵l1∥l2，
∴
-
a
2
=
1
a-3
-
1
2
≠
a
a-3
，解得a=2．
故选：B．
点评：本题考查了直线的斜截式、直线平行与斜率、截距的关系，属于基础题．
练习册系列答案
相关题目
若数列{an}的各项按如下规律排列：
1
1
，
2
1
，
2
2
，
3
1
，
3
2
，
3
3
，
4
1
，
4
2
，
4
3
，
4
4
，…则a2012=
 
．
对于集合A，B，定义A×B={（a，b）|a∈A，b∈B}．
（1）若A={1，2}，B={3，4}，求A×B；
（2）若A×B={（1，2），（2，2）}，求A．B；
（3）若A中有m个元素，B中有n个元素，则A×B中有几个元素？
计算：
（1）（2
7
9
） 
1
2
+（lg5）0+（
27
64
） -
1
3
；
（2）log318-log35+log3
5
6
+2ln
e
．
已知直线L：y=ax+b与曲线T：x=
1
y
+y没有公共点，若平行L的直线与曲线T有且只有一个公共点，则符合条件的直线有几条？
已知两点A（-1，2），B（m，3），求：
（1）直线AB的斜率k；
（2）求直线AB的方程．
已知数列{an}中，a1=1且
1
an+1
=
1
an
+
1
3
（n∈N*），则a10=
 
．
已知命题p：?x∈R，sinx≤1，则￢p为（　　）
A、?x∈R，sinx＞1
B、?x∈R，sinx＞1
C、?x∈R，sinx≥1
D、?x∈R，sinx≥1
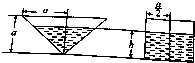一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图，两容器盛有液体的体积正好相等，且液面高均为h，求h．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网