题目内容
3.已知直线?1:ax-y-1=0,?2:x+y+3=0,若?1⊥?2,则a 的值为1.分析 利用两条直线相互垂直的充要条件即可得出.
解答 解:∵?1⊥?2,∴a×(-1)=-1,解得a=1.
故答案为:1.
点评 本题考查了两条直线相互垂直的充要条件,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
18.函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$的定义域为( )
| A. | [-$\frac{1}{2}$,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | [-$\frac{1}{2}$,$\frac{3}{4}$] | D. | (-$\frac{1}{2}$,$\frac{3}{4}$) |
8.经过点M(2,2)且在两轴上截距相等的直线是( )
| A. | x+y=4 | B. | x+y=2 | C. | x=2或y=2 | D. | x+y=4或x=y |
13.设max{p,q}表示p,q两者中的较大者,若函数f(x)=max{1-x,2x},则满足f(x)>4的x的集合为( )
| A. | (-∞,-3)∪(2,+∞) | B. | (-∞,-3) | C. | (-3,2) | D. | (2,+∞) |
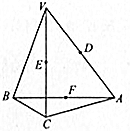 如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.
如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.