题目内容
15.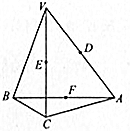 如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.
如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.(1)当DE⊥平面VBC时,判断直线DE与平面ABC的位置关系,并说明理由;
(2)当D、E、F分别为线段VA、VC、AB上的中点,且VC=2BC时,求二面角B-DE-F的余弦值.
分析 (1)证明DE∥AC,即可判断直线DE与平面ABC的位置关系;
(2)BE,DF所成角的大小=二面角B-DE-F的大小,利用余弦定理,即可求解.
解答 解:(1)DE∥平面ABC.
∵VC?平面VBC,DE⊥平面VBC,
∴DE⊥VC,
∵VC⊥平面ABC,∴VC⊥AC,
∵DE⊥VC,VC⊥AC,∴DE∥AC,
∵DE?平面ABC,AC?平面ABC,
∴DE∥平面ABC;
(2)∵DE⊥平面VBC,∴DE⊥BE,DE⊥VB,
∵D,F分别为VA,AB的中点,
∴DF∥VB,∴DE⊥DF,
∴BE,DF所成角的大小=二面角B-DE-F的大小.
∵VC=2BC,∴VE=BC,VB=$\sqrt{5}$BC,∴BE=$\sqrt{2}$BC,
∴cos∠VBE=$\frac{5B{C}^{2}+2B{C}^{2}-B{C}^{2}}{2×\sqrt{5}BC×\sqrt{2}BC}$=$\frac{3\sqrt{10}}{10}$,
∴二面角B-DE-F的余弦值为$\frac{3\sqrt{10}}{10}$.
点评 本题考查直线与平面平行的证明,考查二面角的余弦值的求法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.给出下列函数①y=xcosx②y=sin2x③y=|x2-x|④y=ex-e-x,其中是奇函数的是( )
| A. | ①② | B. | ①④ | C. | ②④ | D. | ③④ |
6.a=${∫}_{0}^{\frac{π}{2}}$(-cosx)dx,则(ax+$\frac{1}{2ax}$)9展开式中,x3项的系数为( )
| A. | -$\frac{21}{2}$ | B. | -$\frac{63}{8}$ | C. | $\frac{63}{8}$ | D. | $\frac{63}{16}$ |
10.若圆C:x2+y2-2x+4y=0上存在两点A,B关于直线l:y=kx-1对称,则k的值为( )
| A. | -1 | B. | -$\frac{3}{2}$ | C. | -$\frac{5}{2}$ | D. | -3 |
20.设a=($\frac{5}{3}$)${\;}^{\frac{1}{6}}$,b=($\frac{3}{5}$)${\;}^{-\frac{1}{5}}$,c=ln$\frac{2}{3}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
7. 执行如图程序,输出的结果为( )
执行如图程序,输出的结果为( )
 执行如图程序,输出的结果为( )
执行如图程序,输出的结果为( )| A. | 513 | B. | 1023 | C. | 1025 | D. | 2047 |