题目内容
设无穷等比数列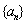 的公比为q,且
的公比为q,且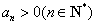 ,
,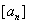 表示不超过实数
表示不超过实数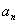 的最大整数(如
的最大整数(如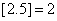 ),记
),记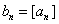 ,数列
,数列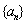 的前
的前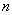 项和为
项和为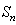 ,数列
,数列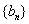 的前
的前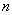 项和为
项和为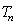 .
.
(Ⅰ)若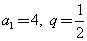 ,求
,求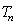 ;
;
(Ⅱ)若对于任意不超过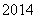 的正整数n,都有
的正整数n,都有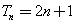 ,证明:
,证明: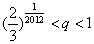 .
.
(Ⅲ)证明: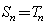 (
(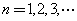 )的充分必要条件为
)的充分必要条件为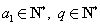 .
.
(Ⅰ)解:由等比数列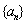 的
的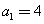 ,
,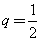 ,
,
得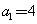 ,
,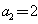 ,
,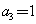 ,且当
,且当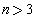 时,
时,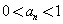 .
.
所以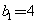 ,
,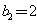 ,
,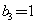 ,且当
,且当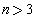 时,
时,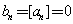 .
.
即 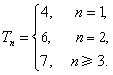
(Ⅱ)证明:因为 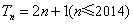 ,
,
所以 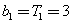 ,
,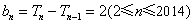 .
.
因为 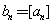 ,
,
所以 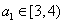 ,
,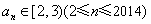 .
.
由 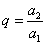 ,得
,得 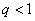 .
.
因为 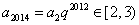 ,
,
所以 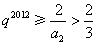 ,
,
所以 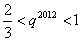 ,即
,即 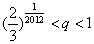 .
.
(Ⅲ)证明:(充分性)因为 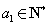 ,
,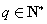 ,
,
所以 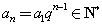 ,
,
所以 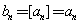 对一切正整数n都成立.
对一切正整数n都成立.
因为 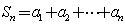 ,
,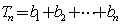 ,
,
所以 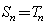 .
.
(必要性)因为对于任意的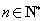 ,
,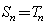 ,
,
当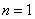 时,由
时,由 ,得
,得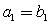 ;
;
当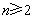 时,由
时,由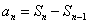 ,
,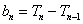 ,得
,得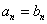 .
.
所以对一切正整数n都有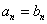 .
.
由 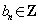 ,
,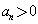 ,得对一切正整数n都有
,得对一切正整数n都有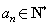 ,
,
所以公比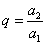 为正有理数.
为正有理数.
假设 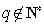 ,令
,令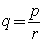 ,其中
,其中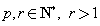 ,且
,且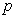 与
与 的最大公约数为1.
的最大公约数为1.
因为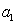 是一个有限整数,
是一个有限整数,
所以必然存在一个整数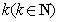 ,使得
,使得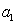 能被
能被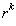 整除,而不能被
整除,而不能被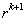 整除.
整除.
又因为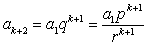 ,且
,且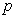 与
与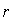 的最大公约数为1.
的最大公约数为1.
所以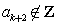 ,这与
,这与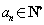 (
(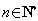 )矛盾.
)矛盾.
所以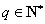 .
.
因此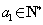 ,
,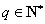 .
.

 的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为 ( )
的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为 ( ) (B)
(B) 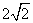 (D)
(D) 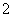
 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 ______.
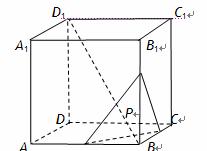
______.  的棱长为
的棱长为 ,动点P在对角线
,动点P在对角线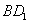 上,过点P作垂直于
上,过点P作垂直于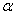 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设 x,则当
x,则当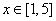 时,函数
时,函数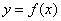 的值域为( )
的值域为( )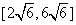 (B)
(B) (C)
(C) (D)
(D)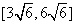
 ,
, ,且
,且 的最小正周期为
的最小正周期为 .
. ,
, ,求
,求 的单调增区间.
的单调增区间. 的解集为
的解集为 B.
B.
 D.
D.
 ,那么
,那么 的最小值为
的最小值为  B.
B. C.
C. D.
D.
 ,
, ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 
 在
在 这
这 个整数中等可能随机产生.
个整数中等可能随机产生. 的值为
的值为 的概率
的概率 ;
; 次后,统计记录了输出
次后,统计记录了输出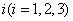 的频数.以下是甲、乙所作频数统计表的部分数据.
的频数.以下是甲、乙所作频数统计表的部分数据.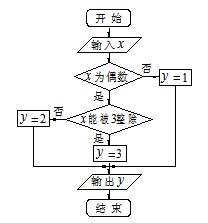
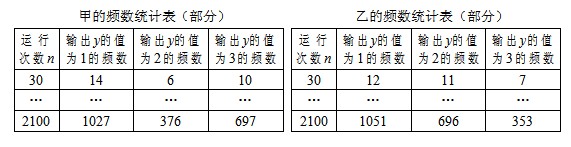
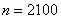 时,根据表中的数据,分别写出甲、乙所编程序各自输出
时,根据表中的数据,分别写出甲、乙所编程序各自输出