题目内容
10.设集合M={x|0≤x≤2},N={y|0≤y≤2}.下列四个图象中能表示从集合M到集合N的函数关系的有( )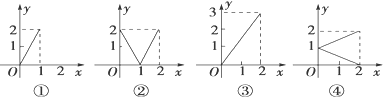
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据函数的定义,对照各个图象可得:图①中集合M中属于区间(1,2]内的元素没有象,不符合题意;图④中集合M的一个元素对应N中的两个元素,也不符合题意;图②③都满足M中任意一个元素,N中有唯一元素与之对应,符合题意.
解答 解:由题意知:M={x|0≤x≤2},N={y|0≤y≤3},
对于图①中,在集合M中区间(1,2]内的元素没有象,比如f(1.5)的值就不存在,所以图①不符合题意;
对于图②中,对于M中任意一个元素,N中有唯一元素与之对应,符合函数的对应法则,故②正确;
对于图③中,对于M中任意一个元素,N中有唯一元素与之对应,且这种对应是一一对应,故③正确;
对于图④中,集合M的一个元素对应N中的两个元素.比如当x=1时,有两个y值与之对应,不符合函数的定义,故④不正确
故选:B.
点评 本题考查的是函数的概念和函数图象的综合类问题.在解答时充分体现了函数概念的知识、函数图象的知识以及问题转化的思想,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.在矩形ABCD中,点E为CD的中点,$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=$\overrightarrow b$,则$\overrightarrow{BE}$=( )
| A. | $-\frac{1}{2}\overrightarrow a-\overrightarrow b$ | B. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ | C. | $-\frac{1}{2}\overrightarrow a+\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a+\overrightarrow b$ |
5.已知函数f(x)=2exln$\sqrt{e}$-kx(e=2.17128…是自然对数的底数)有两个不同的零点,则实数k的取值范围是( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (e,+∞) | D. | (1,+∞) |
2.已知r是实数集,M={x|f(x)=lg(1-$\frac{2}{x}$)},N={x|y=$\sqrt{x-1}$},则(∁RM)∪N=( )
| A. | [0,+∞) | B. | [1,+∞) | C. | [2,+∞) | D. | (1,2) |
19.设无穷等比数列{an}的首项为a1,公比为q,前n项和为Sn,则“a1+q=1”是“$\underset{lim}{n→∞}$Sn=1”成立( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |