题目内容
19.设无穷等比数列{an}的首项为a1,公比为q,前n项和为Sn,则“a1+q=1”是“$\underset{lim}{n→∞}$Sn=1”成立( )| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
分析 根据充要条件的定义,结合无穷缩减数列和的极限值公式,可得答案.
解答 解:当a1<0时,q>1,则$\underset{lim}{n→∞}$Sn=-∞≠1,
故“a1+q=1”是“$\underset{lim}{n→∞}$Sn=1”不充分条件,
若“$\underset{lim}{n→∞}$Sn=1”,则a1=1-q,即“a1+q=1”,
故“a1+q=1”是“$\underset{lim}{n→∞}$Sn=1”必要条件,
综上可得:“a1+q=1”是“$\underset{lim}{n→∞}$Sn=1”成立必要非充分条件,
故选:B
点评 本题考查的知识点是充要条件的定义,无穷缩减数列和的极限值公式,难度中档.

练习册系列答案
相关题目
10.设集合M={x|0≤x≤2},N={y|0≤y≤2}.下列四个图象中能表示从集合M到集合N的函数关系的有( )
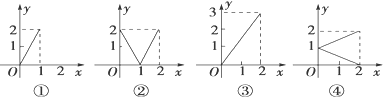

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.若$\overrightarrow{a}$与$\overrightarrow{b}$-$\overrightarrow{c}$都是非零向量,则“$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$”是“$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$)”的( )
| A. | 充分但非必要条件 | B. | 必要但非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
4.若不等式组$\left\{\begin{array}{l}{x-y≥0}\\{2x+y≤2}\\{y≥0}\\{x+y≤a}\end{array}\right.$,表示的平面区域是一个三角形区域,则a的取值范围是( )
| A. | a≥$\frac{4}{3}$ | B. | 0<a≤1 | C. | 1≤a≤$\frac{4}{3}$ | D. | 0<a≤1或a≥$\frac{4}{3}$ |
