题目内容
18.在矩形ABCD中,点E为CD的中点,$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=$\overrightarrow b$,则$\overrightarrow{BE}$=( )| A. | $-\frac{1}{2}\overrightarrow a-\overrightarrow b$ | B. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ | C. | $-\frac{1}{2}\overrightarrow a+\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a+\overrightarrow b$ |
分析 点E为CD的中点,ABCD是矩形,取AB的中点F,则$\overrightarrow{BE}$=$\overrightarrow{FD}$.$\overrightarrow{FD}+\frac{1}{2}\overrightarrow{AB}=\overrightarrow{AC}$,可得答案.
解答 解:由题意:点E为CD的中点,ABCD是矩形,取AB的中点F,则$\overrightarrow{BE}$=$\overrightarrow{FD}$.(如图)
∵$\overrightarrow{FD}+\frac{1}{2}\overrightarrow{AB}=\overrightarrow{AC}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow b$,
∴$\overrightarrow{BE}=\overrightarrow{FD}=\overrightarrow{b}-\frac{1}{2}\overrightarrow{a}$
故选:C.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意平面向量加法法则的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8.下列命题中错误的是( )
| A. | 若命题p为真命题,命题q为假命题,则命题“p∨(¬q)”为真命题 | |
| B. | 命题“若a+b≠7,则a≠2或b≠5”为真命题 | |
| C. | 命题“若x2-x=0,则x=0或x=1”的否命题为“若x2-x=0,则x≠0且x≠1” | |
| D. | 命题p:?x>0,sinx>2x-1,则¬p为?x>0,sinx≤2x-1 |
6.从学号为1至50的高一某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A. | 1,2,3,4,5 | B. | 4,14,24,34,44 | C. | 2,4,6,8,10 | D. | 4,13,22,31,40 |
13.若a>b,则下列正确的是( )
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
1.a2>b2 2.ac>bc 3.ac2>bc2 4.a-c>b-c.
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
3.已知某几何体的三视图如图所示,则这个几何体的体积为( )


| A. | 12π | B. | 45π | C. | 57π | D. | 24π |
10.设集合M={x|0≤x≤2},N={y|0≤y≤2}.下列四个图象中能表示从集合M到集合N的函数关系的有( )
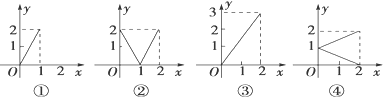

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |