题目内容
15.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),左右焦点分别为F1,F2,C的离心率e=$\frac{{\sqrt{3}}}{2}$,且过P($\sqrt{3},\frac{1}{2}$)点(1)求椭圆C的方程;
(2)若Q点在椭圆C上,且$∠Q{F_1}F_2^{\;}$=30°,求△QF1F2的面积.
分析 (1)由题意的离心率得到a,b的关系,化椭圆方程为$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,把P($\sqrt{3},\frac{1}{2}$)代入求得b2=1,则椭圆方程可求;
(2)在焦点三角形△QF1F2中,由已知结合余弦定理求得:|QF1|=2,代入三角形面积公式可得△QF1F2的面积.
解答 解:(1)∵椭圆的离心率e=$\frac{c}{a}=\frac{\sqrt{3}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{3}{4}$,即a2=4b2,
∴椭圆C的方程可写为$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
把P($\sqrt{3},\frac{1}{2}$)代入C中,得$\frac{3}{4{b}^{2}}+\frac{1}{4{b}^{2}}=1$,∴b2=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)在△QF1F2中,
由余弦定理cos30°=$\frac{|Q{F}_{1}{|}^{2}+(2c)^{2}-|Q{F}_{2}{|}^{2}}{2•2C•|Q{F}_{1}|}$=$\frac{|Q{F}_{1}{|}^{2}+4{c}^{2}-(2a-|Q{F}_{1}|)^{2}}{2•2c•|Q{F}_{1}|}$,
解得:|QF1|=2,
且2c=2$\sqrt{3}$,
∴${S}_{△Q{F}_{1}{F}_{2}}=2×2\sqrt{3}×\frac{1}{2}×sin30°=\sqrt{3}$
点评 本题考查椭圆的标准方程的求法,考查了直线与椭圆位置关系的应用,训练了求解与焦点三角形有关的问题的求解方法,是中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
| A. | 1,2,3,4,5 | B. | 4,14,24,34,44 | C. | 2,4,6,8,10 | D. | 4,13,22,31,40 |

| A. | 12π | B. | 45π | C. | 57π | D. | 24π |
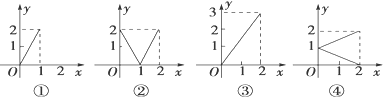
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
| A. | 充分但非必要条件 | B. | 必要但非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |