题目内容
10.对于函数f(x)与g(x),若存在λ∈{x∈R|f(x)=0},μ∈{x∈R|g(x)=0},使得|λ-μ|≤1,则称函数f(x)与g(x)互为“零点密切函数”,现已知函数f(x)=ex-2+x-3与g(x)=x2-ax-x+4互为“零点密切函数”,则实数a的取值范围是[3,4].分析 先求出函数f(x)=ex-2+x-3的零点为x=2,再设g(x)=x2-ax-x+4的零点为β,则|2-β|≤1,从而得到g(x)=x2-ax-x+4必经过点A(0,4),最后利用数形结合法求解即可.
解答 解:函数f(x)=ex-2+x-3的零点为x=2,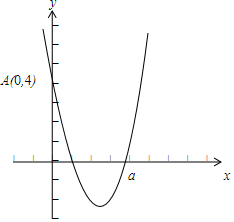
设函数g(x)=x2-ax-x+4的零点为β,
若函数f(x)=ex-2+x-3与g(x)=x2-ax-x+4互为“零点密切函数”,
根据零点关联函数,则|2-β|≤1,∴1≤β≤3,如图,
由于g(x)=x2-ax-x+4必经过点A(0,4),
故要使其零点在区间[1,3]上,则$\left\{\begin{array}{l}{g(1)=1-a-1+4≥0}\\{g(\frac{a+1}{2})=(\frac{a+1}{2})^{2}-a•\frac{a+1}{2}-\frac{a+1}{2}+4≤0}\end{array}\right.$,
解得3≤a≤4.
故答案为:[3,4].
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知$f(x)=\frac{x}{|lnx|}$,若关于x的方程f2(x)-(2m+1)f(x)+m2+m=0,恰好有4个不相等的实数根,则实数m的取值范围为( )
| A. | $(\frac{1}{e},2)∪(2,e)$ | B. | $(\frac{1}{e}+1,e)$ | C. | (e-1,e) | D. | $(\frac{1}{e},e)$ |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F(2,0),双曲线的渐近线y=±$\sqrt{3}$x,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{13}$=1 | B. | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
5.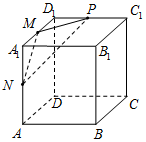 正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
 正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )
正方体ABCD-A1B1C1D1棱长为4,M,N,P分别是棱A1D1,A1A,D1C1的中点,则过M,N,P三点的平面截正方体所得截面的面积为( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |
15.已知圆C:(x-1)2+(y-2)2=25及直线l:(2m+1)x+(m+1)y=7m+4(m∈R),则直线l过的定点及直线与圆相交得的最短弦长分别为( )
| A. | (3,1),$4\sqrt{5}$ | B. | (2,1),$4\sqrt{5}$ | C. | (-3,1),$4\sqrt{3}$ | D. | (2,-1),3$\sqrt{3}$ |
2.已知集合A={x|log${\;}_{\frac{1}{2}}$(x+1)≥-2},B={x|$\frac{x+2}{1-x}$≥2},则 A∩B=( )
| A. | (-1,1) | B. | [0,1) | C. | [0,3] | D. | ∅ |
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-x,x≤0\\-{2^x},x>0\end{array}\right.$,则“f(x)≤0”是“x=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |