题目内容
10.已知点A(1,2)示抛物线y2=4x上一点,过点A作两条直线AD,AE分别交抛物线于点D,E,若AD,AE的斜率分别为kAD,KAE,且kAD+kAE=0,则直线DE的斜率为( )| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 不确定 |
分析 设出直线方程与抛物线方程联立,求出D,E的纵坐标,利用斜率公式,即可得出结论.
解答 解:设AD的斜率为k,则AE的斜率为-k,D(x1,y1),E(x2,y2),
设AD的方程为y-2=k(x-1),
联立$\left\{\begin{array}{l}{y-2=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消去x、整理得:ky2-4y-4k+8=0,
∴y1=-2+$\frac{4}{k}$,
同理y2=-2-$\frac{4}{k}$,
∴y1+y2=-4,
∴直线DE的斜率为$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{4}{{y}_{1}+{y}_{2}}$=-1.
故选:C.
点评 本题是一道直线与抛物线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的右焦点到它的渐进线的距离为( )
| A. | 12 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2 |
18. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 6 | D. | 4$\sqrt{3}$ |
20.设x∈R,则“a=b”是“f(x)=(x+a)|x+b|为奇函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
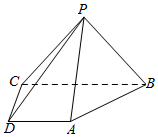 如图,在底面为梯形的四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD⊥CD,AD=CD=2,BC=4.
如图,在底面为梯形的四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD⊥CD,AD=CD=2,BC=4.