题目内容
5.过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A、B两点,若线段AB的长为8,求抛物线的方程.分析 由题意得直线AB的方程为y=x-$\frac{p}{2}$,与抛物线方程消去y关于x的一元二次方程,利用根与系数的关系和抛物线的定义得出|AB|=4p=8,从而解出p的值,则抛物线的方程可求.
解答 解:由题意可知过焦点的直线方程为y=x-$\frac{p}{2}$,联立$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=x-\frac{p}{2}}\end{array}\right.$,
得${x}^{2}-3px+\frac{{p}^{2}}{4}=0$,
设A(x1,y1),B(x2,y2)
根据抛物线的定义,得|AB|=x1+x2+p=4p=8,
解得p=2.
∴抛物线的方程为y2=4x.
点评 本题给出直线与抛物线相交,在已知被截得弦长的情况下求焦参数p的值.着重考查了抛物线的标准方程和直线与圆锥曲线位置关系等知识,属于中档题.

练习册系列答案
相关题目
13.直线$\left\{\begin{array}{l}x=5-3t\\ y=3+\sqrt{3}t\end{array}\right.$(为参数)的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
10.已知点A(1,2)示抛物线y2=4x上一点,过点A作两条直线AD,AE分别交抛物线于点D,E,若AD,AE的斜率分别为kAD,KAE,且kAD+kAE=0,则直线DE的斜率为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 不确定 |
14.设A1,A2分别为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右顶点,若双曲线上存在点M使得两直线斜率${k_{M{A_1}}}{k_{M{A_2}}}<2$,则双曲线C的离心率的取值范围为( )
| A. | $(0,\sqrt{3})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},+∞)$ | D. | (0,3) |
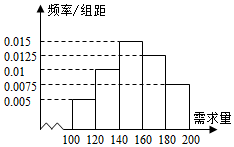 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.