题目内容
2.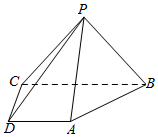 如图,在底面为梯形的四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD⊥CD,AD=CD=2,BC=4.
如图,在底面为梯形的四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD⊥CD,AD=CD=2,BC=4.(Ⅰ)求证:AC⊥PB;
(Ⅱ)若PA=PB,且三棱锥D-PAC的体积为$\frac{2}{3}$,求AP的长.
分析 (I)连结AC,由△ACD为等腰直角三角形可得AC=2$\sqrt{2}$,∠BCA=45°,利用余弦定理解出AB,根据勾股定理的逆定理得出AC⊥AB,由面面垂直的性质得出AC⊥平面PAB,故AC⊥PB;
(II)取AB中点G,连接PG,则PG⊥平面ABCD,于是${V_{D-PAC}}={V_{P-ADC}}=\frac{1}{3}{S_{△ADC}}•PG=\frac{2}{3}$,解出PG,利用勾股定理计算PA.
解答  证明:(Ⅰ)连接AC,因为AD⊥DC,AD=DC=2,所以$AC=2\sqrt{2}$,
证明:(Ⅰ)连接AC,因为AD⊥DC,AD=DC=2,所以$AC=2\sqrt{2}$,
因为AD∥BC,所以∠BCA=∠DAC=45°,
在△ABC中,$AC=2\sqrt{2}$,BC=4
所以AB2=AC2+BC2-2AC•CBcos45°=8,即$AB=2\sqrt{2}$,
所以AC2+AB2=BC2,所以AC⊥AB.
因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
所以AC⊥平面PAB,又PB?平面PAB,
所以AC⊥PB.
解:(Ⅱ)取AB中点G,连接PG,因为PA=PB,所以PG⊥AB,
又平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PG?平面PAB,
所以PG⊥平面ABCD,
所以${V_{D-PAC}}={V_{P-ADC}}=\frac{1}{3}{S_{△ADC}}•PG=\frac{2}{3}$,得PG=1,
所以$PA=\sqrt{A{G^2}+P{G^2}}=\sqrt{3}$.
点评 本题考查了线面垂直的判定与性质,面面垂直的性质,棱锥的体积计算,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.已知实数x、y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+2y+2≥0}\\{4x-y-10≤0}\end{array}\right.$,z=kx+y(k∈R)仅在(4,6)处取得最大值,则k的取值范围是( )
| A. | k>1 | B. | k>-1 | C. | k<-$\frac{1}{2}$ | D. | k<-4 |
13.直线$\left\{\begin{array}{l}x=5-3t\\ y=3+\sqrt{3}t\end{array}\right.$(为参数)的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
10.已知点A(1,2)示抛物线y2=4x上一点,过点A作两条直线AD,AE分别交抛物线于点D,E,若AD,AE的斜率分别为kAD,KAE,且kAD+kAE=0,则直线DE的斜率为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 不确定 |
14.设A1,A2分别为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右顶点,若双曲线上存在点M使得两直线斜率${k_{M{A_1}}}{k_{M{A_2}}}<2$,则双曲线C的离心率的取值范围为( )
| A. | $(0,\sqrt{3})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},+∞)$ | D. | (0,3) |