题目内容
在△ABC中，角A，B，C对应的边是a，b，c，满足2asinA=（2b+c）sinB+（2c+b）sinC
（1）求角A；
（2）若b=2，c=1，D为BC上一点，且CD=2BD，求AD的长．
（1）求角A；
（2）若b=2，c=1，D为BC上一点，且CD=2BD，求AD的长．
考点：余弦定理,正弦定理
专题：解三角形,平面向量及应用
分析：（1）利用正弦定理化简2asinA=（2b+c）sinB+（2c+b）sinC得2a2=（2b+c）b+（2c+b）c，再利用余弦定理求出cosA，从而求出A即可；
（2）如图过D作DE∥AC交AB于E，作DF∥AB交AC于F，根据平行线等分线段定理和向量的加法可得
=
+
，利用向量的数量积公式可求出|
|2=(
+
)2=
2+
•
+
2=
，从而得出|AD|=
．
（2）如图过D作DE∥AC交AB于E，作DF∥AB交AC于F，根据平行线等分线段定理和向量的加法可得
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| 4 |
| 9 |
| AB |
| 4 |
| 9 |
| AB |
| AC |
| 1 |
| 9 |
| AC |
| 4 |
| 9 |
| 2 |
| 3 |
解答：
解：（1）∵在△ABC中，满足
2asinA=（2b+c）sinB+（2c+b）sinC
由正弦定理可得
2a2=（2b+c）b+（2c+b）c，
故cosA=
=-
∵在△ABC中
0＜A＜π
∴A=
．
（2）如图过D作DE∥AC交AB于E，作DF∥AB交AC于F，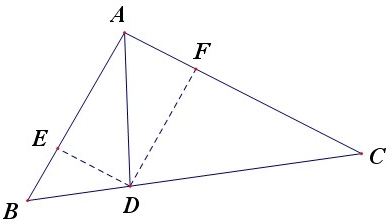
则AEDF是平行四边形，且AE=
AB，AF=
AC，
∴
=
+
，
•
=|
||
|cosA=-1，
∴|
|2=(
+
)2=
2+
•
+
2=
，
∴|AD|=
．
2asinA=（2b+c）sinB+（2c+b）sinC
由正弦定理可得
2a2=（2b+c）b+（2c+b）c，
故cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
∵在△ABC中
0＜A＜π
∴A=
| 2π |
| 3 |
（2）如图过D作DE∥AC交AB于E，作DF∥AB交AC于F，
则AEDF是平行四边形，且AE=
| 2 |
| 3 |
| 1 |
| 3 |
∴
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| AB |
| AC |
| AB |
| AC |
∴|
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| 4 |
| 9 |
| AB |
| 4 |
| 9 |
| AB |
| AC |
| 1 |
| 9 |
| AC |
| 4 |
| 9 |
∴|AD|=
| 2 |
| 3 |
点评：本题主要考查正弦定理和余弦定理得灵活应用，以及向量加法和数量积的几何意义的应用，属于中档题．
练习册系列答案
百分学生作业本题练王系列答案
相关题目
若复数z满足iz=2+4i，则复数z=（ ）
| A、2+4i | B、2-4i |
| C、4-2i | D、4+2i |
如图，景点A在景点B的正北方向2千米处，景点C在景点B的正东方向