题目内容
求y=3sin(
x-
)的对称轴方程,对称中心,单调区间.
| 1 |
| 2 |
| π |
| 4 |
考点:正弦函数的图象
专题:函数的性质及应用
分析:根据三角函数的性质分别进行求解即可.
解答:
解:由
x-
=
+kπ,k∈Z,
解得x=
+2kπ,k∈Z,即函数的对称轴方程为x=
+2kπ,k∈Z,
由
x-
=kπ,k∈Z,解得x=
+2kπ,k∈Z,即函数的对称中心为(
+2kπ,0),k∈Z,
由-
+2kπ≤
x-
≤
+2kπ,
解得-
+4kπ≤x≤
+4kπ,k∈Z,
故函数的单调递增是[-
+4kπ,
+4kπ],k∈Z,
由
+2kπ≤
x-
≤
+2kπ,
解得
+4kπ≤x≤
+4kπ,k∈Z,
故函数的单调递减是[
+4kπ,
+4kπ],k∈Z.
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得x=
| 3π |
| 2 |
| 3π |
| 2 |
由
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
由-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得-
| π |
| 2 |
| 3π |
| 2 |
故函数的单调递增是[-
| π |
| 2 |
| 3π |
| 2 |
由
| π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
解得
| 3π |
| 2 |
| 7π |
| 4 |
故函数的单调递减是[
| 3π |
| 2 |
| 7π |
| 4 |
点评:本题主要考查三角函数的对称性,单调性的求解,要求熟练掌握三角函数的性质.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
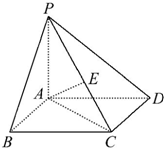 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.