题目内容
空间四边形OABC中,G,H分别是△ABC,△OBC的重心,设
=
,
=
,
=
,试用向量
,
,
表示向量
和
.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
| GH |
考点:空间向量的加减法,空间向量的基本定理及其意义
专题:空间向量及应用
分析:如图所示,G是△ABC的重心,可得
=
+
,
+
,
=
,
=
-
,
=
(
+
),代入即可得出;由
=
-
,
=
,
=
(
+
),代入即可得出.
| OG |
| OC |
| CG |
| OA |
| CG |
| CG |
| 2 |
| 3 |
| CD |
| CD |
| OD |
| OC |
| OD |
| 1 |
| 2 |
| OA |
| OB |
| GH |
| OH |
| OG |
| OH |
| 2 |
| 3 |
| OE |
| OE |
| 1 |
| 2 |
| OB |
| OC |
解答:
解:如图所示,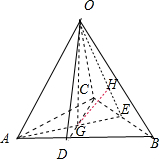
G是△ABC的重心,
∴
=
+
,
+
,
=
,
=
-
,
=
(
+
),
∴
=
+
[
(
+
)-
]
=
+
+
=
+
+
.
=
-
,
=
,
=
(
+
),
∴
=
(
+
)-
(
+
+
)
=-
=-
.

G是△ABC的重心,
∴
| OG |
| OC |
| CG |
| OA |
| CG |
| CG |
| 2 |
| 3 |
| CD |
| CD |
| OD |
| OC |
| OD |
| 1 |
| 2 |
| OA |
| OB |
∴
| OG |
| OC |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| OB |
| OC |
=
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
=
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| c |
| GH |
| OH |
| OG |
| OH |
| 2 |
| 3 |
| OE |
| OE |
| 1 |
| 2 |
| OB |
| OC |
∴
| GH |
| 1 |
| 3 |
| OB |
| OC |
| 1 |
| 3 |
| OA |
| OB |
| OC |
=-
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| a |
点评:本题考查了向量的三角形法则、三角形重心的性质、向量的线性运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧,则( )
| A、D2+E2-4F>0,且F>0 |
| B、D<0,F>0 |
| C、D≠0,F≠0 |
| D、D2>4F,且F<0 |
