题目内容
在△ABC中,若有
=cos2
,则△ABC是 三角形.
| a+b |
| 2b |
| c |
| 2 |
考点:余弦定理
专题:解三角形
分析:利用倍角公式、余弦定理即可得出.
解答:
解:∵cos2
=
,
∴
=cos2
=
,
∴a+b=b+b×
,
化为a2+c2=b2.
∴B=90°.
∴△ABC是直角三角形.
故答案为:直角.
| C |
| 2 |
| 1+cosC |
| 2 |
∴
| a+b |
| 2b |
| c |
| 2 |
| 1+cosC |
| 2 |
∴a+b=b+b×
| a2+b2-c2 |
| 2ab |
化为a2+c2=b2.
∴B=90°.
∴△ABC是直角三角形.
故答案为:直角.
点评:本题考查了倍角公式、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
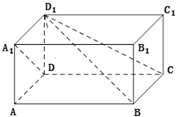 在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.