题目内容
直线y=3x+1与圆x2+y2=4相交于A,B两点,则AB的中点的坐标是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:设A(x1,y1),B(x2,y2),联立直线与圆方程,消去y得到关于x的一元二次方程,利用韦达定理求出x1+x2的值,确定出AB中点横坐标,代入y=3x+1中求出纵坐标,即可确定出AB中点坐标.
解答:
解:设A(x1,y1),B(x2,y2),
联立直线与圆方程得:
,
消去y得:10x2+6x-3=0,
∴x1+x2=-
,即AB中点横坐标为
=-
,
将x=-
代入y=3x+1得:y=
,
则AB中点坐标为(-
,
).
故答案为:(-
,
)
联立直线与圆方程得:
|
消去y得:10x2+6x-3=0,
∴x1+x2=-
| 3 |
| 5 |
| x1+x2 |
| 2 |
| 3 |
| 10 |
将x=-
| 3 |
| 10 |
| 1 |
| 10 |
则AB中点坐标为(-
| 3 |
| 10 |
| 1 |
| 10 |
故答案为:(-
| 3 |
| 10 |
| 1 |
| 10 |
点评:此题考查了直线与圆的位置关系,利用了“设而不求”的解题方法,是一道中档题.

练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1的棱长是1,则直线DA1与平面ACB1间的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线
x-y+2=0与圆x2+y2=2的交点个数有( )个.
| 3 |
| A、0 | B、1 | C、2 | D、不能断定 |
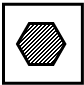 如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒芝麻,它落在阴影区域内的概率为
如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒芝麻,它落在阴影区域内的概率为| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、无法计算 |
