题目内容
光线自点P(-2,3)射出,经x轴反射到圆(x-3)2+(y-4)2=1上的最短路线长为 .
考点:直线和圆的方程的应用
专题:直线与圆
分析:利用圆的对称性,将问题转化为P关于x轴的对称点P′与圆心的距离减去半径即可.
解答:
解:点P(-2,3)关于x轴的对称点为点P′(-2,-3),圆(x-3)2+(y-4)2=1的圆心坐标为C(3,4),半径为1
,所以所求最短路线长为P′C-1=
-1=
-1.
故答案为:
-1.
,所以所求最短路线长为P′C-1=
| (3+2)2+(4+3)2 |
| 74 |
故答案为:
| 74 |
点评:本题考查直线与圆的位置关系,考查圆的对称性考查学生的转化能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则函数y=f[f(x)+1]的零点个数( )
|
| A、2 | B、3 | C、4 | D、5 |
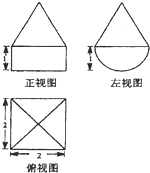 某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为( )A、π+
| ||||
B、2π+
| ||||
C、π+
| ||||
D、2π+
|
下列几何图形的主视图不能是三角形的是( )
| A、三棱柱 | B、圆台 |
| C、四棱锥 | D、圆锥 |