题目内容
19.若复数z满足(z-3)(2-i)=5(i为虚数单位),则z的共轭复数$\overline{z}$为( )| A. | 2+i | B. | 2-i | C. | 5-i | D. | 5+i |
分析 把已知等式变形,利用复数代数形式的乘除运算化简求得z,则$\overline{z}$可求.
解答 解:∵(z-3)(2-i)=5,
∴z-3=$\frac{5}{2-i}=\frac{5(2+i)}{(2-i)(2+i)}=2+i$,
∴z=5+i,
则$\overline{z}=5-i$.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础的计算题.

练习册系列答案
相关题目
9.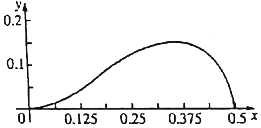 函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )
函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )
 函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )
函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=3 | D. | m=3,n=1 |
7.i是虚数单位,则$\frac{2i}{1+3i}$=( )
| A. | -$\frac{3}{5}$+$\frac{1}{5}$i | B. | $\frac{3}{4}$-$\frac{1}{4}$i | C. | $\frac{3}{5}$+$\frac{1}{5}$i | D. | $\frac{3}{4}$+$\frac{1}{4}$i |
4.“a=$\frac{1}{18}$“是“对任意的正数x,x+$\frac{a}{2x}$≥$\frac{1}{3}$“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.a=20.5,b=logπ3,c=log2sin$\frac{2π}{5}$,则( )
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
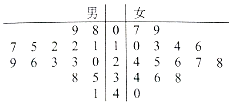 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”. 若
若 ,则实数t的取值范围是( )
,则实数t的取值范围是( ) B.
B. C.
C. D.
D.