题目内容
在四面体ABCD中,平面ABD⊥平面BCD,△ABD为等边三角形,CD⊥BD,∠DBC=30°
(1)求二面角A-DC-B的大小;
(2)求二面角A-BC-D的平面角的正切值;
(3)求二面角D-AB-C的平面角的正切值.
(1)求二面角A-DC-B的大小;
(2)求二面角A-BC-D的平面角的正切值;
(3)求二面角D-AB-C的平面角的正切值.
考点:二面角的平面角及求法
专题:空间角
分析:(1)要求二面角A-DC-B的大小,可找出该二面角的平面角,由面面垂直的性质定理即可得到∠ADB为二面角的平面角,然后解直角三角形得答案;
(2)由平面ABD⊥平面BCD,可在平面ABD内过A作BD的垂线交BD于E点,过E作BC的垂线交BC于F点,由线面垂直的判断得到AF⊥BC,从而得到∠AFE是二面角A-BC-D的平面角,则其正切值可求;
(3)过点D作AB的垂线交AB于G点,连接GC,由△ACD≌△BCD可得AC=BC,进一步说明∠CGD是二面角D-AB-C的平面角,然后通过求解直角三角形得答案.
(2)由平面ABD⊥平面BCD,可在平面ABD内过A作BD的垂线交BD于E点,过E作BC的垂线交BC于F点,由线面垂直的判断得到AF⊥BC,从而得到∠AFE是二面角A-BC-D的平面角,则其正切值可求;
(3)过点D作AB的垂线交AB于G点,连接GC,由△ACD≌△BCD可得AC=BC,进一步说明∠CGD是二面角D-AB-C的平面角,然后通过求解直角三角形得答案.
解答:
解:如图,
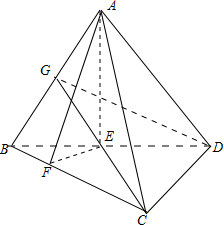 (1)∵平面ABD⊥平面BCD,DC在平面BCD上,而且CD⊥BD,
(1)∵平面ABD⊥平面BCD,DC在平面BCD上,而且CD⊥BD,
∴CD⊥平面ABD,
∴CD⊥AD,
已知CD⊥BD,
∴∠ADB是二面角A-DC-B的平面角,
∵△ABD为等边三角形,
∴二面角A-DC-B=∠ADB=60°;
(2)过点A作BD的垂线交BD于E点,则AE⊥面BCD,AE⊥BC,
过E作BC的垂线交BC于F点,则BC⊥面AEF,
∴AF⊥BC,
∴∠AFE是二面角A-BC-D的平面角,
∴tan∠AFE=
=2
;
(3)过点D作AB的垂线交AB于G点,连接GC,
∵CD⊥平面ABD,△ACD和△BCD均为直角三角形,且BD=AD,CD为公共边,
∴△ACD≌△BCD,
∴AC=BC,
∵ABD为等边三角形,DG⊥AB,
∴G为AB中点,
∴CG⊥AB,
∴∠CGD是二面角D-AB-C的平面角,
∵CD⊥平面ABD,
∴CD⊥DG,
∵∠DBC=30°,设CD=
,
则BD=3,可得DG=
,
∴tan∠CGD=
=
.
 (1)∵平面ABD⊥平面BCD,DC在平面BCD上,而且CD⊥BD,
(1)∵平面ABD⊥平面BCD,DC在平面BCD上,而且CD⊥BD,∴CD⊥平面ABD,
∴CD⊥AD,
已知CD⊥BD,
∴∠ADB是二面角A-DC-B的平面角,
∵△ABD为等边三角形,
∴二面角A-DC-B=∠ADB=60°;
(2)过点A作BD的垂线交BD于E点,则AE⊥面BCD,AE⊥BC,
过E作BC的垂线交BC于F点,则BC⊥面AEF,
∴AF⊥BC,
∴∠AFE是二面角A-BC-D的平面角,
∴tan∠AFE=
| AE |
| EF |
| 3 |
(3)过点D作AB的垂线交AB于G点,连接GC,
∵CD⊥平面ABD,△ACD和△BCD均为直角三角形,且BD=AD,CD为公共边,
∴△ACD≌△BCD,
∴AC=BC,
∵ABD为等边三角形,DG⊥AB,
∴G为AB中点,
∴CG⊥AB,
∴∠CGD是二面角D-AB-C的平面角,
∵CD⊥平面ABD,
∴CD⊥DG,
∵∠DBC=30°,设CD=
| 3 |
则BD=3,可得DG=
| 2 |
| 3 |
| 3 |
∴tan∠CGD=
| CD |
| DG |
| 2 |
| 3 |
点评:本题考查了二面角的平面角的求法,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在区间[-a,a](a>0)上,f(x)只是奇函数,g(x)只是偶函数,那么函数y=f(x)•g(x)( )
| A、只是奇函数 |
| B、只是偶函数 |
| C、既不是奇函数,也不是偶函数 |
| D、可能是奇函数,也可能是偶函数 |
 如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则x,y的值为( )
如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则x,y的值为( )| A、2,4 | B、4,4 |
| C、5,6 | D、6,4 |