题目内容
13．已知等比数列{an}满足a1+a3+a7=22，a5+a7+a11=88，则a7+a9+a13=（ ）| A． | 121 | B． | 154 | C． | 176 | D． | 352 |
分析 由已知求得q2，再由a7+a9+a13=（a5+a7+a11）•q2得答案．
解答 解：在等比数列{an}中，由a1+a3+a7=22，a5+a7+a11=88，
得${q}^{4}=\frac{{a}_{5}+{a}_{7}+{a}_{11}}{{a}_{1}+{a}_{3}+{a}_{7}}=\frac{88}{22}=4$，
∴q2=2，
则a7+a9+a13=（a5+a7+a11）•q2=88×2=176．
故选：C．
点评 本题考查等比数列的通项公式，考查了等比数列的性质，是基础的计算题．
练习册系列答案
阅读快车系列答案
相关题目
3．sin18°•sin78°-cos162°•cos78°等于（ ）
| A． | $-\frac{{\sqrt{3}}}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{2}$ |
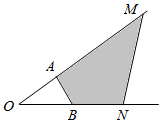如图，A、B分别是射线OM、ON上的点，给出下列以O为起点的向量：①$\overrightarrow{OA}+2\overrightarrow{OB}$；②$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$；③$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$；④$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$；⑤$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$．其中终点落在阴影区域内的向量的序号有（ ）