题目内容
函数f(x)=
,实数a,b,c互不相同,若f(a)=f(b)=f(c)=d,则a+b+c+d的范围为 .
|
考点:分段函数的应用
专题:数形结合,函数的性质及应用
分析:画出函数的图象,不妨设a<b<c,则由题意可得a+b=2,1<d<2,2<c<4,且d越大,c越小,由此可得a+b+c+d的取值范围.
解答:
 解:函数图象如图所示,不妨设a<b<c,则
解:函数图象如图所示,不妨设a<b<c,则
∵实数a,b,c互不相同,f(a)=f(b)=f(c)=d,
∴a+b=2,1<d<2,2<c<4,
∵d越大,c越小,即d→1时,c→4,d→2时,c→2,
∴6<a+b+c+d<7
故答案为:(6,7).
 解:函数图象如图所示,不妨设a<b<c,则
解:函数图象如图所示,不妨设a<b<c,则∵实数a,b,c互不相同,f(a)=f(b)=f(c)=d,
∴a+b=2,1<d<2,2<c<4,
∵d越大,c越小,即d→1时,c→4,d→2时,c→2,
∴6<a+b+c+d<7
故答案为:(6,7).
点评:本小题主要考查分段函数的解析式求法及其图象的作法、函数的值域的应用、函数与方程的综合运用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列函数中定义域为[1,+∞)的是( )
A、y=
| ||||
B、y=
| ||||
C、y=(
| ||||
| D、y=ln(x-1) |
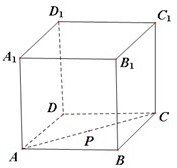 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题: