题目内容
已知向量
=(1,0)与向量
=(-1,
),则向量
与
的夹角是 .
| a |
| b |
| 3 |
| a |
| b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:设
与
的夹角为θ,运用cosθ=
,代入数据求出cosθ的值,再由θ的范围求出θ的值.
| a |
| b |
| ||||
|
|
解答:
解:设向量
与
的夹角为θ,由两个向量的夹角公式可得,
cosθ=
=
=-
.
再由 0°≤θ≤180°可得θ=120°,
故答案为:120°.
| a |
| b |
cosθ=
| ||||
|
|
| -1+0 |
| 1×2 |
| 1 |
| 2 |
再由 0°≤θ≤180°可得θ=120°,
故答案为:120°.
点评:本题主要考查两个向量的夹角公式,两个向量数量积公式,两个向量坐标形式的运算,属于基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F1的直线分别交双曲线的两条渐近线于点P,Q.若点P是线段F1Q的中点,且QF1⊥QF2,则此双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2
,则k的取值范围是( )
| 3 |
A、[-
| ||||||||
B、[-∞,-
| ||||||||
C、[-
| ||||||||
D、[-
|
已知a>0,b>0,4a+b=1,则ab的最大值是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
函数f(x)=sinxcosx的最小正周期为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
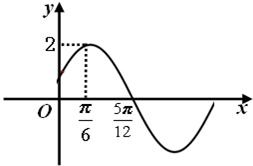 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<