题目内容
函数f(x)=sinxcosx的最小正周期为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
考点:二倍角的正弦,三角函数的周期性及其求法
专题:三角函数的求值
分析:根据二倍角的正弦公式化简函数解析式,再由周期公式求出函数的周期即可.
解答:
解:由题意得,f(x)=sinxcosx=
×2sinxcosx=
sin2x,
所以函数的最小正周期为
=π,
故选:B.
| 1 |
| 2 |
| 1 |
| 2 |
所以函数的最小正周期为
| 2π |
| 2 |
故选:B.
点评:本题考查二倍角的正弦公式,以及三角函数的周期公式应用,熟练掌握公式是解题的关键.

练习册系列答案
相关题目
如果命题“¬P”为假,命题“P∧q”为假,那么则有( )
| A、q为真 |
| B、p∨q为假 |
| C、p∨q为真 |
| D、(¬p)∧(¬q)为真 |
若函数y=f(x)的图象在点(1,f(1))处的切线方程为y=3x-2,则函数g(x)=x2+f(x)的图象在点(1,g(1))处的切线方程为( )
| A、5x-y-3=0 |
| B、5x-y+3=0 |
| C、x-5y+3=0 |
| D、x-5y-3=0 |
下列函数中,是奇函数,又在定义域内为减函数的是( )
A、y=(
| ||
B、y=
| ||
| C、y=-x3 | ||
| D、y=x2 |
sin(
π+x)=( )
| 3 |
| 2 |
| A、sinx | B、cosx |
| C、-sinx | D、-cosx |
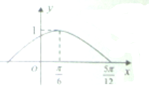 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-