题目内容
3.已知P1(2,-1),P2(0,5)且点P在P1P2的延长线上,$|{\overrightarrow{{P_1}P}}|=2|{\overrightarrow{P{P_2}}}|$,则点P的坐标为(-2,11).分析 设P点(x,y),$|{\overrightarrow{{P_1}P}}|=2|{\overrightarrow{P{P_2}}}|$,由此建立关于x、y的方程组,解之即可得到点P的坐标.
解答 解:∵点P在线段P1P2的延长线上,且$|{\overrightarrow{{P_1}P}}|=2|{\overrightarrow{P{P_2}}}|$,
∴$\overrightarrow{{P}_{1}P}$=-2$\overrightarrow{P{P}_{2}}$
∵P1(2,-1),P2(0,5)
设P点(x,y),
∴$\overrightarrow{{P}_{1}P}$=(x-2,y+1),$\overrightarrow{P{P}_{2}}$=(-x,5-y)
∴$\left\{\begin{array}{l}{x-2=-2(-x)}\\{y+1=-2(5-y)}\end{array}\right.$
∴x=-2,y=11
∴P点的坐标为(-2,11).
故答案为:(-2,11)
点评 本题给出线段P1P2的延长线上满足定比的分点,求该点的坐标.着重考查了向量的坐标运算和两点间距离公式等知识,属于基础题.

练习册系列答案
相关题目
18.已知O为坐标原点,F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,A为C的左顶点,P为C上一点,且PF1⊥x轴,过点A的直线l与线段PF1交于点M,与y轴交于点E,若直线F2M与y轴交点为N,OE=2ON,则C的离心率为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.网络用语“车珠子”,通常是指将一块原料木头通过加工打磨,变成球状珠子的过程,某同学有一圆锥状的木块,想把它“车成珠子”,经测量,该圆锥状木块的底面直径为12cm,体积为96πcm3,假设条件理想,他能成功,则该珠子的体积最大值是( )
| A. | 36πcm3 | B. | 12πcm3 | C. | 9πcm3 | D. | 72πcm3 |
15.某种电路开关闭合后会出现红灯或绿灯闪烁,已知开关第一次闭合后出现红灯的概率为0.5,两次闭合后都出现红灯的概率为0.2,则在第一次闭合后出现红灯的条件下第二次闭合后出现红灯的概率为( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.5 |
12.设函数f(x)=-x2+14x+15,数列{an}满足an=f(n),n∈N+,数列{an}的前n项和Sn最大时,n=( )
| A. | 14 | B. | 15 | C. | 14或15 | D. | 15或16 |
 已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.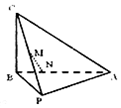 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.