题目内容
11.已知倾斜角为α的直线l与直线x+2y-3=0垂直,则$\frac{sinα-cosα}{sinα+cosα}$=$\frac{1}{3}$.分析 由直线垂直的性质求出tanα=2,由此利用同角三角函数关系式能求出$\frac{sinα-cosα}{sinα+cosα}$的值.
解答 解:∵倾斜角为α的直线l与直线x+2y-3=0垂直,
∴tanα=2,
∴$\frac{sinα-cosα}{sinα+cosα}$=$\frac{tanα-1}{tanα+1}$=$\frac{2-1}{2+1}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意三角函数性质的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.如果二次函数y=x2+4x+(m+3)有两个不同的零点,则m的取值范围是( )
| A. | (-∞,1) | B. | (-2,6) | C. | [-2,6] | D. | {-2,6} |
16.函数$f(x)=\left\{\begin{array}{l}2x-{x^2},0≤x≤3\\{x^2}+6x,-2≤x<0\end{array}\right.$的值域是( )
| A. | [-8,1] | B. | [-8,-3] | C. | R | D. | [-9,1] |
3.下列不等式中,解集是空集的是( )
| A. | x2-x+1>0 | B. | 2x-x2>5 | C. | -2x2+x+1>0 | D. | x2+x>2 |
1.已知函数$f(x)=tan({2x+\frac{π}{3}})$,则$f({\frac{25π}{6}})$=( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
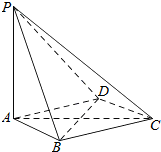 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.