题目内容
1.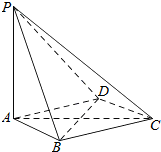 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值.
分析 (1)推导出AC⊥BD,PA⊥BD,由此能证明BD⊥平面PAC.
(2)以O为坐标原点,建立空间直角坐标系,利用向量法能求出PB与AC所成角的余弦值.
解答 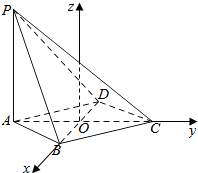 证明:(1)∵四边形ABCD是菱形,∴AC⊥BD,
证明:(1)∵四边形ABCD是菱形,∴AC⊥BD,
又∵PA⊥平面ABCD,∴PA⊥BD,
∴BD⊥平面PAC.
解:(2)设AC∩BD=O,∵∠BAD=60°,PA=PB=2,
∴BO=1,AO=CO=$\sqrt{3}$,
如图,以O为坐标原点,建立空间直角坐标系,
则P(0,-$\sqrt{3}$,2),A(0,-$\sqrt{3}$,0),B(1,0,0),C(0,$\sqrt{3}$,0),
∴$\overrightarrow{PB}$=(1,$\sqrt{3}$,-2),$\overrightarrow{AC}$=(0,2$\sqrt{3}$,0),
设PB与AC所成角为θ,
则cosθ=$\frac{|\overrightarrow{PB}•\overrightarrow{AC}|}{|\overrightarrow{PB}|•|\overrightarrow{AC}|}$=$\frac{6}{2\sqrt{2}×2\sqrt{3}}$=$\frac{\sqrt{6}}{4}$.
∴PB与AC所成角的余弦值为$\frac{\sqrt{6}}{4}$.
点评 本题考查线面垂直的证明,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
11.红、黄两支队员实力相当的乒乓球队进行擂台赛,已知每支队均有六名队员,规则如下:每支队给队员编号1,2,3,4,5,6,第一场双方1号比赛,负者被淘汰.然后负方队的2号与胜方队的1号再比赛,负者又被淘汰,一直这样进行下去,直到一方队员全被淘汰时,另一方获胜,则红队有3名队员波淘汰且最后战胜黄队的概率是( )
| A. | $\frac{1}{11}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{10}{11}$ |
9.函数f(x)=loga(x3-2ax)(a>0且a≠1)在(4,+∞)上单调递增,则a的取值范围是( )
| A. | 1<a≤4 | B. | 1<a≤8 | C. | 1<a≤12 | D. | 1<a≤24 |
6.已知p:0<a<4,q:函数y=x2-ax+a的值恒为正,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.圆x2+y2-2x+4y=0的圆心到直线x-y=0的距离为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |