题目内容
1.已知函数$f(x)=tan({2x+\frac{π}{3}})$,则$f({\frac{25π}{6}})$=( )| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
分析 利用函数性质及诱导公式求解.
解答 解:∵函数$f(x)=tan({2x+\frac{π}{3}})$,
∴$f({\frac{25π}{6}})$=tan($\frac{25π}{3}+\frac{π}{3}$)=tan$\frac{2π}{3}$=-tan$\frac{π}{3}$=-$\sqrt{3}$.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意诱导公式的合理运用.

练习册系列答案
相关题目
13.已知等差数列{an}的前n项的和为Sn,若a5+a6=10,则S10=( )
| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
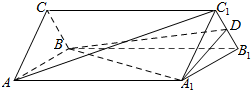 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.