题目内容
19．函数$y=\sqrt{{{log}_{\frac{1}{3}}}x}$的定义域是（0，1]．分析 由被开方数大于等于0，然后利用对数函数的单调性及真数大于0求出x的范围，写出集合区间形式即为函数的定义域．
解答 解：由log${\;}_{\frac{1}{3}}$x≥0，
解得：0＜x≤1
∴函数$y=\sqrt{{{log}_{\frac{1}{3}}}x}$的定义域是（0，1]．
故答案为：（0，1]．
点评 本题考查了函数的定义域及其求法，考查了对数不等式的解法，是基础题．
练习册系列答案
相关题目
9．已知f（x）是定义在R上周期为4的奇函数，当x∈[-2，0）时，f（x）=2x+log2（-x），则f（2017）=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -2 | D． | 2 |
7．已知集合A={1，2}，则A的真子集的个数为（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
14．复数$z=\frac{i^3}{i-1}$，则其共轭复数$\overline z$在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
4．已知sinα=$\frac{3}{5}$，则cos（π-2α）=（ ）
| A． | -$\frac{4}{5}$ | B． | -$\frac{7}{25}$ | C． | $\frac{7}{25}$ | D． | $\frac{4}{5}$ |
11．
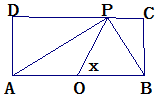如图，长方形的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD，与DA运动，记∠BOP=x，将动点P到A，B两点距离之和表示为函数f（x），则f（x）的图象大致为（ ）
如图，长方形的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD，与DA运动，记∠BOP=x，将动点P到A，B两点距离之和表示为函数f（x），则f（x）的图象大致为（ ）| A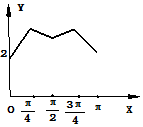． |  | B． |  | ||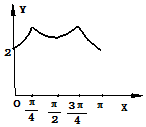
| C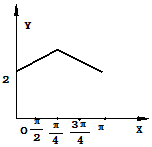． |  | D． |  |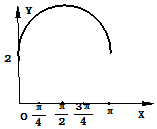
8．等比数列{an}的各项均为正数，且a5a6+a2a9=18，则log3a1+log3a2+…+log3a10的值为（ ）
| A． | 12 | B． | 10 | C． | 8 | D． | 2+log35 |
9．已知F1，F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，椭圆C上存在点P使∠F1PF2为钝角，则椭圆C的离心率的取值范围是（ ）
| A． | （$\frac{\sqrt{2}}{2}$，1） | B． | （$\frac{1}{2}$，1） | C． | （0，$\frac{\sqrt{2}}{2}$） | D． | （0，$\frac{1}{2}$） |