题目内容
9.已知f(x)是定义在R上周期为4的奇函数,当x∈[-2,0)时,f(x)=2x+log2(-x),则f(2017)=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
分析 由已知中f(x)是定义在R上周期为4的奇函数,可得f(2017)=f(1)=-f(-1),进而得到答案.
解答 解:∵f(x)是定义在R上周期为4的奇函数,
∴f(2017)=f(1)=-f(-1),
由当x∈[-2,0)时,f(x)=2x+log2(-x),
∴f(-1)=$\frac{1}{2}$,
故f(2017)=-$\frac{1}{2}$,
故选:A.
点评 本题考查的知识点是函数的周期性,函数的奇偶性,函数求值,难度不大,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
19.若函数f(x)=g(x)+x2为奇函数,且f(1)=1,则函数g(x)的解析式可能为( )
| A. | y=x3 | B. | y=2x3-x2 | C. | y=2x3+x2 | D. | y=x5-x2 |
20.设关于x的不等式|f(x)|+|g(x)|<a的解集为A,关于x的不等式|f(x)+g(x)|<a的解集为B,则集合A,B满足( )
| A. | A⊆B | B. | B⊆A | C. | B?A | D. | A?B |
17.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点和虚轴上的一个端点分别为F,A,点P为双曲线C左支上一点,若△APF周长的最小值为6b,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{56}}{8}$ | B. | $\frac{\sqrt{85}}{7}$ | C. | $\frac{\sqrt{85}}{6}$ | D. | $\frac{\sqrt{13}}{3}$ |
14.在区间[1,7]上任取一个数,这个数在区间[5,8]上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
1.已知函数f(x+1)=x2-x,则f(2)=( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
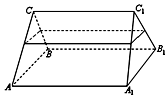 如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )
如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )