题目内容
已知f(x)为偶函数,且f(2+x)=f(2-x),当-2≤x≤0时,f(x)=2x;若n∈N*,an=f(n),则a2013=( )
| A、2009 | ||
| B、-2009 | ||
C、
| ||
D、
|
考点:函数的周期性
专题:函数的性质及应用
分析:根据条件求出函数的周期性,利用函数奇偶性和周期性之间的关系即可得到结论.
解答:
解:∵f(x)为偶函数,且f(2+x)=f(2-x),
∴且f(2+x)=f(2-x)=f(x-2),
即f(4+x)=f(x),
∴函数的周期是4.
∴an=f(n)的周期也是4,
∴a2013=a1=f(1),
∵f(x)为偶函数,当-2≤x≤0时,f(x)=2x;
∴f(-1)=f(1)=2-1=
即a2013=a1=f(1)=
,
故选:D.
∴且f(2+x)=f(2-x)=f(x-2),
即f(4+x)=f(x),
∴函数的周期是4.
∴an=f(n)的周期也是4,
∴a2013=a1=f(1),
∵f(x)为偶函数,当-2≤x≤0时,f(x)=2x;
∴f(-1)=f(1)=2-1=
| 1 |
| 2 |
即a2013=a1=f(1)=
| 1 |
| 2 |
故选:D.
点评:本题主要考查函数奇偶性和对称轴之间的关系得到函数的周期性,考查函数性质的综合应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
已知三角形满足sinA:sinB:sinC=5:3:7,则这个三角形的最大角为( )
| A、150° | B、135° |
| C、120° | D、90° |
已知三点A(a,2),B(5,1),C(-4,2a)在同一直线上,则a的值是( )
| A、1或2 | ||
B、2或
| ||
C、2或-
| ||
| D、1或-2 |
椭圆16x2+25y2=400的长轴和短轴的长、离心率分别是( )
A、10,8,
| ||
B、5,4,
| ||
C、10,8,
| ||
D、5,4,
|
在△ABC中,a=
-1,b=
+1,c=2
,则角C等于( )
| 3 |
| 3 |
| 2 |
| A、30° | B、60° |
| C、90° | D、120° |
数列{an}中,an=-2n2+9n+3,则此数列最大项的值是( )
| A、3 | ||
| B、13 | ||
C、13
| ||
| D、12 |
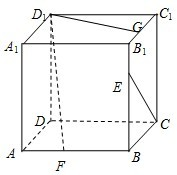 已知正方体ABCD-A1B1C1D1,点E、F、G分别是棱B1B、AB和B1C1上的动点,观察直线CE与D1F,CE与D1G.
已知正方体ABCD-A1B1C1D1,点E、F、G分别是棱B1B、AB和B1C1上的动点,观察直线CE与D1F,CE与D1G.