题目内容
若x＜1，则x+
的最大值是 ．
| 1 |
| x-1 |
考点：基本不等式
专题：计算题,不等式的解法及应用
分析：法一：令f（x）=x+
，x＜1．利用导数研究其单调性极值与最值即可得出．
法二：变形利用基本不等式的性质即可．
| 1 |
| x-1 |
法二：变形利用基本不等式的性质即可．
解答：
解：法一：令f（x）=x+
，x＜1．
则f′（x）=1-
，
令f′（x）=0，∵x＜1，∴x=0．
当x＜0时，f′（x）＞0，函数f（x）单调递增；
当0＜x＜1时，f′（x）＜0，函数f（x）单调递减．
∴当x=0时，函数f（x）取得极大值，即最大值，且为f（0）=-1．
法二：∵x＜1，∴1-x＞0．
∴x+
=-[（-x+1）+
-1]≤-（2
-1）=-1，
当且仅当x=0时取等号．
因此x+
的最大值是-1．
故答案为：-1．
| 1 |
| x-1 |
则f′（x）=1-
| 1 |
| (x-1)2 |
令f′（x）=0，∵x＜1，∴x=0．
当x＜0时，f′（x）＞0，函数f（x）单调递增；
当0＜x＜1时，f′（x）＜0，函数f（x）单调递减．
∴当x=0时，函数f（x）取得极大值，即最大值，且为f（0）=-1．
法二：∵x＜1，∴1-x＞0．
∴x+
| 1 |
| x-1 |
| 1 |
| 1-x |
(1-x)•
|
当且仅当x=0时取等号．
因此x+
| 1 |
| x-1 |
故答案为：-1．
点评：本题考查了利用导数研究其单调性极值与最值，以及运用基本不等式求最值，属于基础题．
练习册系列答案
相关题目
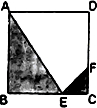某人定制了一批地砖，每块地转（如图所示）是边长为1米的正方形ABCD，点EF分别在边BC和CD上，且CE=CF，△CFE、△ABE和四边形AEFD均由单一材料制成，制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元．问点E在什么位置时，每块地转所需的材料费用最省？
已知圆F1：（x+1）2+y2=16，定点F2（1，0），动圆M过点F2，且与圆F1相内切．