题目内容
17.已知函数f(x)=(x-m)(ex-1)+x+1,m∈R.(1)求f(x)在[0,1]上的最小值;
(2)若m为整数,当x>0时,f(x)>0恒成立,求m的最大值.
分析 (1)求出函数的导函数,讨论m的取值,研究函数在[0,1]上的单调性进行求解即可得到结论.
(2)把当x>0时f(x)>0恒成立,转化为m<$\frac{x+1}{{e}^{x}-1}$+x,构造函数g(x)=$\frac{x+1}{{e}^{x}-1}$+x,利用导数求得函数g(x)的最小值的范围得答案.
解答 解:(1)函数的导数f′(x)=(ex-1)+(x-m)ex+1=(x+1-m)ex,
由f′(x)=0得x=m-1,
由f′(x)>0得x>m-1,此时函数f(x)为增函数,
由f′(x)<0得x<m-1,此时函数f(x)为减函数,
即当x=m-1时,函数取得极小值,f(m-1)=)=-(em-1-1)+m,.
若m-1<0即m<1时,函数f(x)在[0,1]上是增函数,此时函数的最小值为f(0)=1,
若m-1>1即m>2时,函数f(x)在[0,1]上是减函数,此时函数的最小值为f(1)=(1-m)(e-1)+2,
若0≤m-1≤1,即1≤m≤2时,函数的最小值为f(m-1)=)=-(em-1-1)+m;
(2)当x>0时,ex-1>0,
∴不等式f(x)>0,等价为(x-m)(ex-1)+x+1>0,即m<$\frac{x+1}{{e}^{x}-1}$+x ①
令g(x)=$\frac{x+1}{{e}^{x}-1}$+x,则g′(x)=$\frac{{e}^{x}({e}^{x}-x-2)}{({e}^{x}-1)^{2}}$,
函数h(x)=ex-x-2在(0,+∞)上单调递增,而h(1)<0,h(2)>0,
∴h(x)在(0,+∞)上存在唯一的零点,
故g′(x)在(0,+∞)上存在唯一的零点.
设此零点为a,则a∈(1,2).
当x∈(0,a)时,g′(x)<0;当x∈(a,+∞)时,g′(x)>0;
∴g(x)在(0,+∞)上的最小值为g(a).由g′(a)=0,可得ea=a+2,
∴g(a)=a+1∈(2,3),
由于①式等价于m<g(a).∴m<2,
故整数m的最大值为2.
点评 本题考查了利用导数求函数的最小值,以及函数恒成立问题,着重考查了数学转化思想方法,考查了函数最值的求法,利用参数分离法以及分类讨论的思想是解决本题的关键.综合性较强,难度较大.

| A. | $\frac{2}{3}<m≤\frac{3}{4}$ | B. | $\frac{3}{4}<m≤\frac{4}{5}$ | C. | $\frac{2}{3}<m<\frac{3}{4}$ | D. | $\frac{3}{4}<m<\frac{4}{5}$ |
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
| A. | 1-2i | B. | -$\frac{11}{5}$+2i | C. | 1+2i | D. | -4+2i |
| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
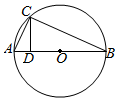 圆O上一点C在直径AB上的射影为D,AD=4,DB=8,求CD,AC和BC的长.
圆O上一点C在直径AB上的射影为D,AD=4,DB=8,求CD,AC和BC的长.