题目内容
7.已知函数y=f(x)=|x-1|-mx,若关于x的不等式f(x)<0解集中的整数恰为3个,则实数m的取值范围为 ( )| A. | $\frac{2}{3}<m≤\frac{3}{4}$ | B. | $\frac{3}{4}<m≤\frac{4}{5}$ | C. | $\frac{2}{3}<m<\frac{3}{4}$ | D. | $\frac{3}{4}<m<\frac{4}{5}$ |
分析 由f(x)<0得|x-1|<mx,构造函数,作出两个函数的图象得到不等式关系进行求解即可.
解答 解:由f(x)<0得|x-1|-mx<0,即|x-1|<mx,
设g(x)=|x-1|,h(x)=mx.
作出g(x)的图象如图:
若|x-1|<mx解集中的整数恰为3个,
则x=1,2,3是解集中的三个整数,
则满足$\left\{\begin{array}{l}{h(3)>g(3)}\\{h(4)≤g(4)}\end{array}\right.$,即$\left\{\begin{array}{l}{3m>2}\\{4m≤3}\end{array}\right.$,
则$\left\{\begin{array}{l}{m>\frac{2}{3}}\\{m≤\frac{3}{4}}\end{array}\right.$,即$\frac{2}{3}<m≤\frac{3}{4}$,
故选:A
点评 本题主要考查函数与方程的应用,根据不等式整数根的个数,结合数形结合建立不等式关系是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.经过点(2,1),且渐近线与圆x2+(y-2)2=1相切的双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{\frac{11}{3}}$-$\frac{{y}^{2}}{11}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | $\frac{{y}^{2}}{\frac{11}{3}}$-$\frac{{x}^{2}}{11}$=1 | D. | $\frac{{y}^{2}}{11}$-$\frac{{x}^{2}}{\frac{11}{3}}$=1 |
2.已知双曲线$\frac{{x}^{2}}{k}+\frac{{y}^{2}}{6+k}=1$的实轴长为4,则双曲线的渐近线方程为( )
| A. | y=$±\frac{1}{2}x$ | B. | y=±x | C. | y=±2x | D. | y=±$\sqrt{2}x$ |
16.若关于x的不等式a-ax>ex(2x-1)(a>-1)有且仅有两个整数解,则实数a的取值范围为( )
| A. | (-$\frac{3}{4}$,$\frac{5}{3{e}^{2}}$] | B. | (-1,$\frac{3}{2e}$] | C. | (-$\frac{3}{2e}$,-$\frac{5}{3{e}^{2}}$] | D. | (-$\frac{3}{4}$,-$\frac{5}{3{e}^{2}}$) |
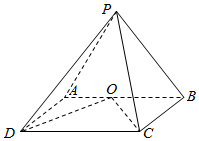 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.