题目内容
计算下列各式:
(1)
÷
;
(2)(2
)0+2-2•(2
)-
-(0.01)0.5.
(1)
| 3 | a
| ||||
|
(2)(2
| 3 |
| 5 |
| 1 |
| 4 |
| 1 |
| 2 |
考点:有理数指数幂的化简求值
专题:计算题
分析:(1)把根式化为分数指数幂,按照幂的运算法则进行计算即可;
(2)化为分数形式,按照幂的运算法则进行计算即可.
(2)化为分数形式,按照幂的运算法则进行计算即可.
解答:
解:(1)原式=(a
•a-
)
÷(a-
•a
)
=a(
-
)×
÷a(-
+
)×
=a÷a-
=a1-(-
)
=a
=a
;
(2)原式=1+
•(
)-
-(0.01)
=1+
•(
)
-(0.1)2×
=1+
•
-0.1
=1+
-
=1
.
| 9 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 7 |
| 3 |
| 13 |
| 3×3 |
| 1 |
| 2 |
=a(
| 9 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 7 |
| 3 |
| 13 |
| 9 |
| 1 |
| 2 |
=a÷a-
| 4 |
| 9 |
=a1-(-
| 4 |
| 9 |
=a
| 13 |
| 9 |
=a
| 9 | a4 |
(2)原式=1+
| 1 |
| 22 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+
| 1 |
| 4 |
| 2 |
| 3 |
=1+
| 1 |
| 6 |
| 1 |
| 10 |
=1
| 1 |
| 15 |
点评:本题考查了根式化为分数指数幂的运算问题,也考查了幂的运算法则的应用问题,是基础题目.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知命题p:x2+2x-3>0;命题q:x>a,且?q的一个充分不必要条件是?p,则实数a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-3] |
| C、[-1,+∞) |
| D、[1,+∞) |
函数f(x)=xsinx2在区间[0,4]上的零点个数为( )
| A、4 | B、5 | C、6 | D、7 |
函数f(x)=
(a>0且a≠1)是(-∞,+∞)上的减函数,则a的取值范围是( )
|
| A、(1,+∞) | ||
B、(0,
| ||
C、[
| ||
| D、(0,1) |
函数f(x)=x2-2lnx的单调减区间是( )
| A、(0,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-1,1) |
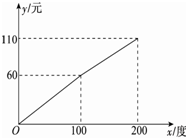 某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示.
某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示.