Question

6．已知向量$\overrightarrow a=（x，y）$，若实数x，y满足$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3\end{array}\right.$，则$|{\overrightarrow a}|$的最大值是（　　）

• A． $\sqrt{73}$
• B． $\frac{{5\sqrt{2}}}{2}$
• C． $\sqrt{43}$
• D． $3\sqrt{2}$

Answer 1

分析 由约束条件作出可行域，由$|{\overrightarrow a}|$的几何意义，即可行域内动点到原点的距离，数形结合得到最优解，联立方程组求得最优解的坐标，代入两点间的距离公式得答案．

解答 解：由约束条件$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3\end{array}\right.$作出可行域如图，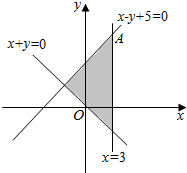

∵$\overrightarrow a=（x，y）$，∴$|\overrightarrow{a}|=\sqrt{{x}^{2}+{y}^{2}}$，
其几何意义为可行域内动点到原点的距离，
由图可知，A到原点距离最大．
联立$\left\{\begin{array}{l}{x=3}\\{x-y+5=0}\end{array}\right.$，解得A（3，8），
∴$|{\overrightarrow a}|$的最大值是$\sqrt{{3}^{2}+{8}^{2}}=\sqrt{73}$．
故选：A．

点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．